voliuf.narod.ru

8.Математика и физика Flash

Внимание! Для работы с этой лекцией необходимы учебные файлы, которые Вы можете загрузить

здесь.

Перед тем, как работать с этой лекцией, вы можете загрузить chapter8-final.fla с сайта http://www.friendsofed.com/books/studio/flash_mx/code.html.

Надеюсь, что вы разберетесь во всем материале этой лекции, так как я постарался изложить его максимально доходчиво, но все же настоятельно рекомендую вам повторить весь материал, изученный до сих пор.

Сначала скажу, что авторы данной книги не несут ответственности за материал по математике и физике. Мы будем рассматривать различные математические и физические принципы, и кое-что из того, с чем вы встретитесь, могло отсутствовать в учебниках по математике и физике, которыми вы когда-либо пользовались. Некоторые из концепций были упрощены для использования во Flash: убраны те части уравнений, с которыми мы не будем работать, а определения иногда звучат почти еретически. В некоторых случаях я значительно отклонился от реальности, дабы получить быстрый, простой и очевидный результат. Одним словом, если вы хотите изучать физику и математику в их стандартном представлении, лучше обратитесь к соответствующим учебникам. Если же вы хотите создавать впечатляющие эффекты с помощью математики и физики во Flash - читайте дальше:

Введение в тригонометрию

Нет, не убегайте из комнаты с дикими криками! Эта наука совсем не страшна. Шутки в сторону, это на самом деле один из наиболее важных предметов, который понадобится вам для изучения управления фильмами и фигурами, и, по большому счету, не представляет особой сложности. Многие люди говорят: "Я могу сделать многое с помощью ActionScript, однако в математике я не силен". Я всегда отвечаю таким людям: "Вам это и не нужно. Flash реализует за вас все математические вычисления". И это правда. Вам понадобится только умение мыслить логически и принимать решения, глядя на полученный промежуточный результат. Я изучал эти подходы и концепции по ходу дела и не вижу, почему бы вам не поступить так же.

Прежде всего, что же такое тригонометрия? Из самого названия можно сделать вывод, что это наука о треугольниках. Говоря более конкретно, в данной науке рассматриваются связи между углами и сторонами треугольника. Мы будем иметь дело только с прямоугольными треугольниками, т.е. с теми, один угол которых равен в точности 90 градусам.

У прямоугольного треугольника есть несколько очень полезных особенностей. Если вы сталкивались с теоремой Пифагора, то знаете, что квадрат гипотенузы равен сумме квадратов двух других сторон, т.е. катетов. Видите, вы уже кое в чем разбираетесь! Однако дальше - больше.

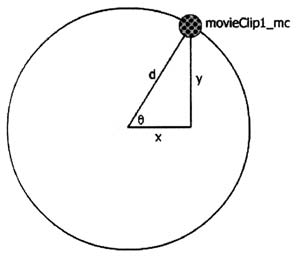
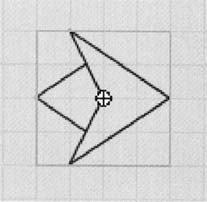
Теперь введем три небольших слова, которые вы будете использовать практически постоянно: sin, cos и tan. Каждое из них характеризует соотношение между двумя сторонамами треугольника. (Кстати, sin - сокращение от "синус", cos - от "косинус", а tan - от "тангенс".) Рассмотрим следующий рисунок.

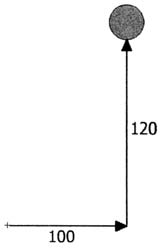
Символ θ - это греческая буква "тета", как правило, используемая для обозначения углов. Мы будем использовать ее для обозначения левого нижнего угла треугольника. x, y, и d обозначают длину сторон треугольника. С точки зрения q, y будет противолежащей стороной, x - прилежащей стороной, а d - гипотенузой.

Сначала рассмотрим sin.

Sin определяется как длина противолежащей стороны, деленная на гипотенузу. В нашем случае можно сказать, что sinq равен y/d. Например, если y равна 10 и d равна 30, то отношением будет 10/30, или 0,3333:

Каждый угол будет иметь свое собственное отношение противолежащей стороны к гипотенузе. Размер треугольника не имеет значения, только угол. Возьмем угол в 30°. Его отношение противолежащего катета к гипотенузе равно 0,5. Всегда. Поэтому мы говорим: sin 30° = 0,5. Следовательно, если y равно 10, а d равно 20, отношение даст в результате 0,5, и отсюда q равен 30°. Если вы знаете, что q равен 30°, а y равно 10, вы можете вычислить d, которое будет равно 20. Наконец, если вы знаете, что d равно 20, то y будет равно 10.

Другими словами, если вам известны хотя бы два атрибута, вы всегда можете вычислить третий, при этом необходимо просто знать отношения, которые формирует каждый угол. Самое интересное, что все это встроено во Flash! Все, что вам нужно, это написать Math.sin(angle) - и вы получите дробь для данного угла.

Теперь перейдем к косинусу. Cos - это отношение прилежащего катета к гипотенузе. Поэтому в нашем случае cos q = x/d.

Наконец, тангенс - это отношение противолежащего катета к прилежащему. В нашем треугольнике tan q = y/x.

Как же использовать эти строки во Flash? Они обычно используются для кругового движения фильма. Кругового? Мы ведь говорили о треугольниках: Что ж, посмотрите на следующий рисунок.

Нам нужно, чтобы movieClip1_mc двигался по круговой траектории, совершая полный оборот по часовой стрелке, начиная со своей текущей позиции. Здесь d - это радиус круга, и он всегда постоянен. Давайте предположим, что он равен 100, а углом будет q. Теперь, в каждый момент времени мы будем знать d и q, поэтому с помощью sin мы сможем найти y, а с помощью cos можно вычислить x. Формулы для этих вычислений следующие.

x = sin q * d
y = cos q * d

Вооружившись этими значениями, мы можем найти параметры _x и _y нашего фильма. Я знаю, что вы уже хотите поскорее приступить к работе и опробовать изложенный здесь материал на движении объектов, но здесь существует еще один момент. Flash вычисляет все углы для использования в математических функциях в радианах, а не в градусах. Это просто еще один способ разделения круга на секторы. Я не буду долго рассказывать о радианах, скажу лишь, что один радиан равен примерно 57,29578 градусов. Интересно, правда? Для облегчения запоминания: круг образован углом в 360 градусов, что равно 2p радианам. Следовательно, один радиан - это p180 градусов. Это соотношение, которое мы будем использовать в большинстве случаев для преобразования радианов в углы. Запишите следующие формулы на вашей шпаргалке.

Градусы = радианы*180/Math.p

Радианы = градусы*Math.p/180

Ознакомившись с основной теорией, перейдем к работе непосредственно во Flash. Мы применим концепции тригонометрии в нашем ActionScript, чтобы обеспечить движение фильма по строго круговой траектории. Если вам нужен файл с примером, его имя - circular_motion.fla.

Движение по кругу

Откройте новый основной фильм и создайте в нем клип. Он может содержать любой рисунок, однако не делайте этот рисунок слишком большим, чтобы было достаточно места для круговой траектории. Назовите его инстанс movieClip1_mc:
Теперь мы создадим функцию onEnterFrame. Первое, что мы будем в ней делать, это увеличивать угол theta. Введите следующий код в новый слой с именем Actions:
this.onEnterFrame = function() {
var theta = 0;
theta++;
};
Далее нам нужно преобразовать theta в радианы. Мы используем для этого другую переменную с именем rad.
this.onEnterFrame = function() {
    var theta = 0;
    theta++;
    var rad = theta*(Math.PI/180);
};
Теперь, если мы умножим cos угла theta на радиус воображаемой окружности (d=100 на предыдущем рисунке), то получим параметр _x. Мы будем прибавлять к этому вычислению 275, так как x=275 является центром экрана (это определяется разрешением вашего фильма, которое по умолчанию равно 550х400 пикселям). В результате фильм будет двигаться вперед и назад по оси x в центре экрана, а не в точке (0,0), которая является левым верхним углом рабочего места.
this.onEnterFrame = function() {
    var theta = 0;
    theta++;
    var rad = theta*(Math.PI/180);
    movieClip1_mc._x = (Math.cos(rad)*100) +275;
};
После этого мы делаем то же самое с параметром _y с помощью sin угла theta, умноженного на 100, и затем прибавляем 200 для расположения фильма по середине экрана. Добавьте следующий код.
this.onEnterFrame = function() {
    var theta = 0;
    theta++;
    var rad = theta*Math.PI/180;
    movieClip1_mc._x = Math.cos(rad)*100+275;
    movieClip1_mc._y = Math.sin(rad)*100+200;
};
Запустите фильм. Вы увидите, что movieClip1_mc совершает круговое движение.
Для большего понимания того, как код реализует движение по окружности, добавьте в функцию следующий код рисования API.
this.onEnterFrame = function() {
    var theta = 0;
    theta++;
    var rad = theta*Math.PI/180;
    movieClip1_mc._x = Math.cos(rad)*100+275;
    movieClip1_mc._y = Math.sin (rad)*100+200;
    clear();
    linestyle(1, 0, 100);
    moveTo(275, 200);
    lineTo (movieClip1_mc._x, movieClip1_mc ._y) ;
    lineTo(movieClip1_mc._x, 200);
    lineTo(275, 200);
};

Теперь вычисляемый треугольник будет хорошо виден.

Вот так. Вы использовали простейшие тригонометрические выражения для создания движения. Не слишком сложно, не так ли? В данном примере мы знали угол и одну сторону треугольника и использовали эту информацию для вычисления длины других сторон. Мы также можем сделать обратное: если мы уже знаем две стороны треугольника, мы можем вычислить любые углы. Это делается с помощью функций arc - arcsin, arccos и arctan (также обозначаются asin, acos и atan). Это функции, противоположные функциям sin, cos и tan. Вместо того чтобы брать угол и получать соотношение, они берут соотношение и получают угол, который формирует это отношение.

Безусловно, наиболее часто используется atan. Эта функция очень полезна для нахождения угла между двумя точками, такими как фильмы. Мы можем легко вычислить расстояние X и Y между двумя фильмами. Это может быть использовано для рисования двух сторон прямоугольного треугольника. 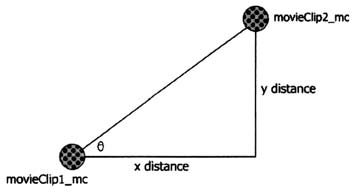Помня, что tan - это отношение противолежащего катета к прилежащему, мы видим, что tan является функцией, связанной с отношением двух катетов, без гипотенузы. Рассмотрим следующий рисунок.

Здесь у нас есть два фильма. Мы можем найти расстояние x так:

dx = movieClip2_mc._x - movieClip1_mc._x;

и расстояние y таким образом:

dy = movieClip2_mc._y - movieClip1_mc._y;

Теперь, если мы получим отношение dy/dx и возьмем atan этого отношения, то узнаем, что угол равен q.

Flash дает нам две функции для вычисления atan: Math.atan (y/x) и Math.atan2 (y,x). Упрощенная версия atan представляет свое отношение y/x в качестве аргумента. Новая версия atan2 использует отдельные значения y и x. Я настоятельно рекомендую вам использовать версию atan2, так как это решит множество проблем, связанных с отрицательными значениями и углами. Большинство разработчиков используют исключительно эту версию.

Не забывайте о том, что Math.atan2, как и все остальные математические функции, будет возвращать угол в радианах. Если вам нужны градусы, можете преобразовать результат соответствующим образом.

Чтобы завершить введение в тригонометрию, разберемся, как использовать Math.atan2 для выполнения очень полезной функции, которая требуется довольно часто - поворот фильма по направлению к определенной цели.

Вы смотрите на меня?

Это небольшое упражнение даст очень простой, но полезный результат: фильм будет всегда указывать на курсор мыши, динамически поворачиваясь вслед за ним. Мы также "привяжем" фильм к мыши. Запустите ship.swf, чтобы увидеть результат в действии.

Откройте новый основной фильм. Прежде всего в нем нужно создать клип, который будет играть роль указателя. Наш круглый футбольный мяч для этого не годится, поэтому создайте такой рисунок, который будет указывать определенное направление, например, космический корабль. В системе координат Flash, угол 0 градусов направлен вправо, а величина угла возрастает в направлении часовой стрелки, поэтому независимо от того, что вы нарисовали, сделайте так, чтобы рисунок с самого начала указывал в правую сторону. Как обычно, назовите инстанс именем movieClip1_mc:
Теперь нужно решить, на что будет указывать наш рисунок. Так как мы создаем этот файл с нуля, единственный объект, двигающийся по экрану - это указатель мыши. Его мы и будем использовать в качестве цели, на которую будет указывать наш фильм. Расстоянием xdistance будет расстояние от позиции _x фильма до this._xmouse, а расстоянием ydistance будет расстояние между movieClip1_mc._y и this._ymouse. Добавьте новый слой Actions, и настройте его так же, как и в последний раз в функции onEnterFrame.
this.onEnterFrame = function() {
var dx = this._xmouse-movieClip1_mc._x;
var dy = this._ymouse-movieClip1_mc._y;
};
Затем мы будем вычислять угол между movieClip1 и мышью с помощью математической функции atan2.
this.onEnterFrame = function() {
    var dx = this._xmouse-movieClip1_rnc._x;
    var dy = this._ymouse-movieClip1_mc._y;
    var angle = Math.atan2(dy, dx);
};
Теперь мы можем использовать этот угол для поворота movieClip1. Однако нужно помнить, что параметр _rotation фильма выражается в градусах, а не в радианах. Поэтому нам нужно добавить преобразование из градусов в радианы, рассмотренное ранее.
this.onEnterFrame = function() {
    var dx = this._xmouse-movieClip1_mc._x;
    var dy = this._ymouse-movieClip1_mc._y;
    var angle = Math.atan2(dy, dx);
    movieClip1_mc._rotation = angle*180/Math.PI;
};
Запустите фильм. Ваш рисунок будет постоянно поворачиваться за указателем мыши.
Закройте пробный фильм. Давайте подумаем, как сделать это все динамически. Так как расстояния X и Y (dx и dy) постоянно вычисляются, мы можем не только заставить рисунок постоянно "смотреть" на указатель мыши, но еще сделать так, что рисунок будет все время двигаться за указателем мыши. Вставьте небольшой отрывок кода, который сейчас уже должен быть вам понятен.
this.onEnterFrame = function() {
    var dx = this._xmouse-movieClip1_mc._x;
    var dy = this._ymouse-movieClip1_mc._y;
    var angle = Math.atan2(dy, dx);
    movieClipl_mc._rotation = angle*180/Math.PI;
    movieClipl_mc._x += (_root._xmouse-movieClip1_mc._x)/10;
    movieClipl_mc._y += (_root._ymouse-movieClip1_mc._y)/10;
};
Запустите фильм еще раз. Вы увидите, что фильм будет следовать за указателем мыши как потерявшийся щенок. Если вы не представляете себе, как можно реализовать игру на основе этого эффекта:что ж, продолжим.
Сохраните фильм с осмысленным именем. Позже в этой лекции он нам еще понадобится.

Основные принципы движения

Мы рассмотрели довольно сложную теорию, однако мы будем использовать концепции тригонометрии снова и снова, поэтому не забывайте о них.

Что только уже не было на нашем экране: и корабли, и снаряды, и мячи: В каждом случае мы просто изменяли параметры _x и/или _y фильма. Постоянно, кадр за кадром прибавляя это значение к позиции фильма, мы создавали плавное движение. Мы также рассматривали скорость по направлению (velocity). Мы знаем, что объект имеет определенную скорость speed, скажем, 10 пикселей в кадр, но в каком направлении он движется? Можно определить это направление в углах, например можно сказать, что объект движется со скоростью 15 пикселей в секунду под углом в 45 градусов.

Напомним, что во Flash 0 градусов является самой правой точкой окружности, и величина угла растет по часовой стрелке.

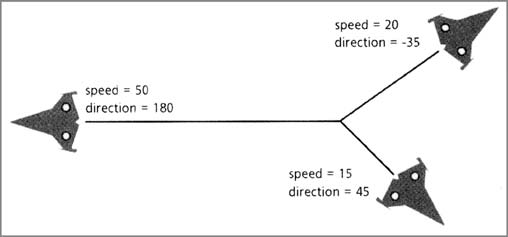
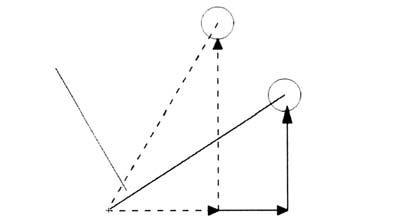
Возвращаясь к нашему примеру, предположим, что объект движется со скоростью 20 (мы всегда будем иметь в виду количество пикселей в кадр) и под углом -35 градусов (это те же 35 градусов, только против часовой стрелки на рисунке выше). Или же представим, что корабль "летит" со скоростью 50 под углом 180 градусов. На следующем рисунке показаны все три случая.

Линии на рисунке называются векторами. Они обозначают как направление движения, так и скорость, а следовательно, и скорость по направлению: чем длиннее линия, тем больше скорость. Это также можно считать расстоянием, которое преодолевает объект за один кадр.

Теперь давайте вернемся к первому примеру. Объект движется со скоростью 15 ppf (пикселей в кадр) под углом 45 градусов. Чтобы правильно реализовать это движение во Flash, необходимо знать, какое значение нужно прибавлять к параметрам _x и _y в каждом кадре. Другими словами, нужно знать скорости по направлениям X и Y. Чтобы определить эти скорости, нужно найти способ преобразования "скорости плюс угол" в "скорость по направлению X, скорость по направлению Y". Как раз здесь находит применение тригонометрия. Рассмотрим следующий рисунок.

В одном кадре корабль перемещается на 15 пикселей под углом 45 градусов. Можно также сказать, что он перемещается на х пикселей по оси x (скорость по направлению X) и на y пикселей по оси y (скорость по направлению Y). В результате мы получили прямоугольный треугольник. На самом деле он выглядит почти так же, как и на рисунке, изображавшем движение объекта по круговой траектории. Единственная разница заключается в использовании значений для вычисления скорости по направлению, а не абсолютной скорости. Формулы для реализации этих вычислений такие же.

x_velocity = cos(angle)*speed
y_velocity = sin(angle)*speed

Во Flash мы будем использовать velX и velY для представления скоростей X и Y. Нам также понадобится преобразовывать углы в радианы. Вот как это выглядит в ActionScript.

var angle = 45;
var speed = 15;
var rad = angle*Math.PI/180;
velX = Math.cos(rad)*speed;
velY = Math.sin(rad)*speed;

Теперь мы можем просто добавить функцию onEnterFrame для прибавления скоростей к позиции вездесущего movieClip1, и все готово.

movieclip1_mc.onEnterFrame = function() {
this._x += velX;
this._y += velY;
};

Безусловно, заставить один фильм двигаться на заданной скорости по заданному направлению не является динамической задачей. Для исследования этого метода мы продолжим использование последнего созданного нами FLA, т.е. объекта, следующего за мышью (в данном случае - космический кораблик). В последнем упражнении мы использовали формулу уменьшения для обеспечения следования фильма за указателем мыши. Если бы корабль находился далеко от указателя мыши, он бы начал перемещение быстро и затем замедлялся по мере приближения к указателю. В некоторых случаях более реалистично смотрится объект, который двигается с постоянной скоростью.

Равномерная скорость

Откройте файл, над которым вы работали в предыдущем упражнении. Для освежения программы в памяти приведем весь имеющийся код.
this.onEnterFrame = function() {
    var dx = this._xmouse-movieClip1_mc._x;
    var dy = this._ymouse-movieClip1_mc._y;
    var angle = Math.atan2(dy, dx) ;
    movieClip1_mc._rotation = angle*180/Math.PI;
    movieClip1_mc._x += (_root._xmouse-movieClip1_mc._x)/10;
    movieClip1_mc._y += (_root._ymouse-movieClip1_mc._y)/10;
};
Мы оставим первые пять строк, которые обеспечивают вращение movieClip1 в нужном направлении. После этого мы просто добавим в код вычисление скоростей X и Y по углу. Они заменят последние две строки, которые перемещали фильм. Обновите код следующим образом.
var speed = 5;
this.onEnterFrame = function() {
    var dx = this._xmouse-movieClip1_mc._x;
    var dy = this._ymouse-movieClip1_mc._y;
    var angle = Math.atan2(dy, dx);
    movieClipl_mc._rotation = angle*180/Math.PI;
    var velX = Math.cos(angle)*speed;
    var velY = Math.sin(angle)*speed;
    movieClip1_mc._x += velX;
    movieClip1_mc._y += velY;
};

Обратите внимание на то, что я также объявил переменную speed для использования в вычислениях. Всегда предпочтительно сначала объявлять переменную, а затем использовать ее в вычислениях, в отличие от реализации кодом отдельного значения. Если вам нужно будет впоследствии изменить значение speed, вам не придется искать его среди различных выражений и функций.
Запустив фильм, вы увидите, что он следует за указателем мыши с постоянной скоростью, независимо от того, в каком месте он находится на экране.
Однако вы могли заметить, что фильм, достигнув указателя мыши, перемещается на несколько пикселей за него и после этого поворачивается на 180 градусов в противоположную сторону и снова начинает движение. Это происходит постоянно, поэтому стрелка указывает то в одну, то в другую сторону. Этот недостаток можно устранить с помощью обнаружения коллизий на основе расстояний. (Видите, весь пройденный материал начинает взаимодействовать!) Нам нужно просто вычислить среднее расстояние между фильмом и указателем мыши. Если оно окажется меньшим, чем определенное расстояние, движение прекратится. Это расстояние численно будет таким же, как и средняя скорость.
Введите окончательный код.
var speed = 5;
this.onEnterFrame = function() {
    var dx = this._xmouse-movieClip1_mc._x;
    var dy = this._ymouse-movieClip1_mc._y;
    var angle = Math.atan2(dy, dx);
    movieClip1_mc._rotation = angle*180/Math.PI;
    var dist = Math.sqrt(dx*dx+dy*dy);
    if (dist>speed) {
      velX = Math.cos(angle)*speed;
      velY = Math.sin(angle)*speed;
      movieClip1_mc._x += velX;
      movieClip1_mc._y += velY;
    }
};
Запустите фильм. Если расстояние между указателем мыши и фильмом больше, чем speed, фильм будет двигаться. В противном случае он остановится и будет ожидать дальнейших действий.

Если вы хотите, чтобы по достижении фильмом цели что-нибудь происходило, например, взрыв корабля или нечто подобное, вы можете вставить дополнительный код в блок else после блока кода if. (Вам также может понадобиться настроить фильм так, чтобы точка регистрации была на конце стрелки. Помните, что положение фильма определяется только его точкой регистрации. Если она находится в середине стрелки, то проверка на коллизию будет осуществляться именно по этой точке.)
Сохраните фильм и оставьте его открытым для следующего упражнения.

Ускорение

В предыдущем упражнении мы рассматривали постоянную скорость. В реальных условиях, если на светофоре вы нажимаете на педаль газа, то скорость автомобиля не станет моментально равна 100 км/ч. При скорости 0 км/ч вы нажимаете педаль газа. По прошествии секунды скорость вашего автомобиля достигнет 5 км/ч, еще через секунду скорость будет равна 10 км/ч и т.д. Ваша скорость будет увеличиваться на 5 км/ч каждую секунду. Это увеличение скорости называется ускорением. В нашем примере ускорение равно 5 км/ч в секунду, т.к. каждую секунду скорость увеличивается на 5 км/ч. Довольно просто. Теперь попробуем применить это во Flash.

Увеличиваем скорость

Откройте ваш фильм из предыдущего упражнения (если он еще не открыт). Расположите movieClip1 как можно левее на рабочем месте. Удалите весь имеющийся код в слое Actions и вставьте этот небольшой отрывок кода в кадр 1:
var accel = .05;
var velX = 0;
movieClip1_mc.onEnterFrame = function() {
this._x += velX;
velX += accel;
};
Запустите фильм. Вы увидите, что фильм будет двигаться слева направо, постепенно ускоряясь по мере движения.
Этот код довольно прост, но полезен. Мы постоянно обновляем переменную velX (и, следовательно, позицию _x movieClip1) значением переменной ускорения accel. По мере выполнения кода в каждом кадре скорость по направлению увеличивается, и наш объект ускоряется при движении слева направо.

Только что я упомянул термин увеличивающаяся скорость. Вот как мы обычно себе это представляем. Акселератор вашего автомобиля предназначен для того, чтобы автомобиль ехал быстрее, ведь так? Но нам следует быть более точными и сказать, что ускорение на самом деле изменяет скорость. Можно выразиться еще точнее и сказать, что ускорение изменяет скорость по направлению, так как ускорение всегда имеет свое направление. В этом мы сейчас разберемся.

Если направление ускорения совпадает с текущей скоростью, эта скорость будет увеличиваться.

Если ускорение направлено в противоположную сторону относительно скорости по направлению, оно уменьшит эту скорость. Если вы, двигаясь со скоростью 50 км/ч, включите задний ход и нажмете педаль газа, я гарантирую вам, что ваша скорость очень быстро уменьшится. Если двигатель и трансмиссия вашего автомобиля уцелеют, ваша скорость в итоге станет нулевой и затем отрицательной - вы поедете в обратную сторону. Безусловно, обычный автомобиль не предназначен для таких "трюков", поэтому если вы представите себе астронавта, который использует реактивные двигатели для управления движением корабля, вы сможете быстрее разобраться в физике происходящего.

Каждая сила, которая изменяет позицию объекта, может быть интерпретирована как некое ускорение данного объекта. Двигатель автомобиля, ускоритель ракеты, гравитация, магнетизм, ветер - все это ускоряет объект в определенном направлении. Давайте рассмотрим одну из этих сил и применим ее во Flash. Мы будем моделировать эффект гравитации для фильма. Сначала выполним небольшое упражнение, чтобы уяснить принципы, на которых базируется эффект, а затем перейдем к более основательному проекту, в котором применим знания, полученные при создании игры Asteroids.

Гравитация

Откройте исходный файл gravity_base.fla и обратите внимание на код в кадре 1 слоя actions. Вам может показаться, что там много кода. Однако он реализует непростую функциональность, о которой мы еще не рассказывали. В коде так же использован изученный до сих пор материал. Просмотрите внимательно этот код и убедитесь в том, что вы знаете, для чего предназначена каждая его строка.
На данный момент вы можете "зацеплять" шарик мышью и "бросать" его в любое место экрана. Скорость шарика по направлению постепенно уменьшается со временем. Теперь мы добавим сюда еще одну функциональность, которая будет симулировать гравитацию для шарика. На шарик будут действовать две силы, оказывая влияние на его движение: трение и гравитация.
Я уже говорил, что гравитация, как и всякая другая сила, ускоряет объект в определенном направлении. В каком направлении? Конечно вниз! Так как направления вниз и вверх лежат лишь на одной оси y, мы можем интерпретировать гравитацию как прибавления определенной скорости, направленной вниз по направлению y, т.е. velY. Это делается одной строкой в первом выражении if функции move.
function move() {
if   (!this.dragging) {
    this.velY += grav;
    this.velX*= friction;
    this.velY*= friction;
    this._x += this.velX;
    this._y += this.velY;
Нам нужно также переместиться вверх и определить значение для grav в функции init.
grav = 1;
Запустите фильм. Зацепите шарик мышью и бросьте его. Вы увидите, как эффект гравитации влияет на скорость шарика.
Здесь velY изначально равна 0, так как не имеет определения (Flash довольно милостив в этом отношении, так как многие другие языки восприняли бы это как ошибку), но затем к velY прибавляется 1, так как grav = 1. Итак, в начале фильма шарик начинает движение по направлению к низу экрана со скоростью 1. В каждом кадре значение velY увеличивается на 1, поэтому шарик ускоряется до тех пор, пока не окажется внизу экрана, отскакивает и затем меняет направление движения. Красиво, не так ли? Шарик начинает движение вверх, так как его скорость по направлению Y поменяла направление (стала отрицательной).

Предположим, что в точке отскока шарик двигается со скоростью 20 пикселей в секунду в нижнем направлении. Он отскакивает, и значением velY становится -20, однако grav все еще прибавляет 1 к velY в каждом кадре. Таким образом, velY примет значения -19, -18, -17 и т.д. до тех пор, пока не обратится в ноль. grav все еще добавляет 1 (это происходит постоянно), поэтому шарик опять начнет движение вниз. Здесь происходит то же самое, что и при подбрасывании вверх реального предмета.

Теперь в нашем багаже достаточно знаний. Совместим изученное в проекте Flash с движущимися объектами. Мы создадим старую школьную игру Atari Asteroids 1979 года.

Проект №1: Asteroids

Сначала определим, что мы хотим реализовать.

С помощью двух клавиш можно поворачивать корабль по или против часовой стрелки.
При нажатии клавиши двигателя корабль начинает движение в направлении, по которому он расположен.
Чем дольше вы держите клавишу двигателя, тем выше скорость корабля.
Если развернуть корабль и начать ускорение в обратную сторону, его скорость уменьшится, затем корабль остановится и начнет движение в противоположном направлении.
При нажатии другой клавиши, корабль выпустит снаряд в направлении, которое он указывает.
По всему экрану летают астероиды, и в случае столкновения вы проигрываете и погибаете.
Если снаряд попадает в астероид, последний раскалывается пополам на достаточно мелкие части, после чего они просто исчезают.

Хотите - верьте, хотите - нет, мы изучили почти весь материал для реализации всех этих возможностей. Нам просто нужно связать вместе все то, что мы изучили до сих пор.

Сначала создадим стереотипный корабль для расстрела астероидов в виде фильма, экспортируем его в ActionScript с использованием идентификатора ship. Здесь важно помнить, что объект должен указывать вправо.

Я также создал второй кадр в этом фильме, изображающий пламя из сопел корабля. Он будет использоваться для визуального обозначения того, что у корабля работают двигатели. Убедитесь в том, что в обоих кадрах есть действие stop, чтобы фильм не начал их проигрывание вперед и назад.

После этого создайте астероид, являющийся просто фигурой с заливкой, величина которой в несколько раз больше, чем сам корабль. Также экспортируйте его с использованием имени asteroid.
Наконец, создайте снаряд с именем shot.
Убедитесь, что слева на рабочем месте нет никаких объектов, так как данные фильмы будут добавляться динамически.
В кадре 1 мы начнем с функции init. Не забудьте первым делом вызвать функцию.
init();
function init() {
    // set constants for stage borders
    if (!stagelsSet) {
      LEFT = 0;
      TOP = 0;
      BOTTOM = Stage.height;
      RIGHT = Stage.width;
      stageIsSet = true;
    }
    // how many ships do we start with?
    livesLeft = 5;
    // set how many asteroids to begin with
    maxAst = 3;
    ast_array = new Array() ;
    // asteroids and shots will be in their own mc's
      to prevent depth conflicts
    createEmptyMovieClip("astField_mc", 0) ;
    createEmptyMovieClip("shots_mc", 1);
    // create asteroids and ship
    astInit();
    shipInit();
    stop();
}

В данном коде достаточно много комментариев, однако мы все равно его разберем. Сначала устанавливаем константы для размера рабочего места (RIGHT, LEFT, TOP, BOTTOM). После этого устанавливаем переменную stageIsSet на значение true, что предотвратит повторный запуск кода при перезапуске игры.

После этого мы определяем, сколько астероидов и какое количество жизней будет в начале игры, а также создаем массив для хранения в нем фильмов астероидов.

Следующие две строки являются альтернативным способом решения проблем дубликатной глубины, с которыми мы сталкивались ранее. Здесь мы будем держать все астероиды внутри одного фильма, а все снаряды - в другом фильме. Так как несущие фильмы сами по себе находятся на разных глубинах (0 и 1), глубины астероидов не будут пересекаться с глубинами снарядов и наоборот. Мы просто проверяем, что при добавлении фильмов со снарядами или астероидами они помещаются в соответствующий несущий фильм.

Затем вызываем функцию инициализации наших астероидов, а также функцию инициализации корабля. Объекты разделены на две функции, поэтому их можно вызывать впоследствии для создания большего количества астероидов, либо для восстановления уничтоженного корабля.

Наконец, останавливаем фильм на данном кадре.
Теперь давайте посмотрим на функцию astInit.
function astInit( ) {
    // create a number of asteroids
    astIndex = 0;
    while (astIndex<maxAst) {
      createAst();
    }
}

Все, что в ней реализуется - это цикл от нуля до количества созданных астероидов, а также повторное выполнение функции createAst, что создает один астероид. Рассмотрим данную функцию.
Функция createAst такова.
function createAst() {
    // put one asteroid on stage and initialize
       its properties and methods
    ast_mc = astField_mc.attachMovie("asteroid",
       "ast"+astIndex, astIndex++) ;
    ast_mc._rotation = Math.random()*360;
    ast_mc.velX = Math.random()*6-3;
    ast_mc.velY = Math.random()*6-3;
    ast_mc.onEnterFrame = astMove;
    // push this asteroid onto the asteroid array
    ast_array.push(ast_mc);
    // return a reference to this asteroid
    return ast_mc;
}

Здесь инстанс астероида добавляется в фильм astField_mc. (Помните, все они должны оставаться в этом фильме для предотвращения проблем с глубинами.) С помощью временной переменной ast_mc мы вращаем его случайным образом, присваиваем ему скорость по направлению и управляющий элемент onEnterFrame и помещаем в массив ast_array. Полезно хранить ссылки на все астероиды в массиве, чтобы можно было обрабатывать массив циклом для проверки на попадание.

Наконец, возвращаем ссылку на вновь созданный астероид. Несмотря на то, что мы проигнорировали ее в функции astInit, она пригодится в дальнейшем.
Следующим шагом является функция shipInit ().
function shipInit() {
    // put a ship on stage and initialize
        its properties and methods
    attachMovie("ship", "ship_mc", 2);
    ship_mc._x = RIGHT/2;
    ship_mc._y = BOTTOM/2;
    ship_mc.velX = 0;
    ship_mc.velY = 0;
    ship_mc.onKeyDown = control;
    ship_mc.onKeyUp = decontrol;
    ship_mc.onEnterFrame = move;
    Key.addListener(ship_mc);
    rotate = 0;
    thrust = 0;
}

Она добавляет инстанс фильма корабля, присваивая ему имя ship_mc. После этого он позиционируется, присваивается его скорость и несколько функций поддержки событий, фильм становится приемником событий Key, а также устанавливаются на 0 две другие переменные - rotate и thrust - для обеспечения неподвижности корабля при его появлении.

Теперь рассмотрим функции, присвоенные нами управляющим элементам onKeyDown и onKeyUp - control и decontrol.
Функция control.
function control() {
    // check which key was pressed and
        control ship accordingly
    switch (Key.getCode()) {
    case Key.LEFT :
      rotate = -1;
      break;
    case Key.RIGHT :
      rotate = 1;
      break;
    case Key.UP :
      thrust = .3;
      ship_mc.gotoAndStop(2);
      break;
    case Key.SPACE :
      shoot();
      break;
    }
}

Она представляет собой просто выражение switch. Если нажаты клавиши LEFT или RIGHT, она устанавливает переменную rotate на значения -1 или +1.

При нажатой клавише UP переменная thrust устанавливается на значение .3 (При желании вы можете изменить это значение. Я пришел к нему методом проб и ошибок - оно обеспечивает хорошую динамику корабля). Здесь мы также отправляем корабль в кадр 2 и отображаем выпускаемые им ракеты. Далее мы увидим, как переменные rotate и thrust используются для управления движением корабля.

Наконец, если нажата клавиша SPACE, выполняем функцию shoot.
Все вышеописанное происходит при нажатых клавишах. При отпускании клавиши нужно, чтобы корабль прекращал ускорение двигателями (и визуально нужно отобразить это) и прекращал поворот (если таковой имел место).
Все довольно просто.

function decontrol() {
    // no key is pressed, so no thrust or rotation
    rotate = 0;
    thrust = 0;
    ship_mc.gotoAndStop(1); }
Продолжая работать над функциями корабля, мы установили управляющий элемент onEnterFrame для функции движения. Давайте разберем ее.
function move() {
    // rotate ship
    if (rotate) {
      this._rotation += rotate*5;
    }
    // move ship
    if (thrust) {
      // convert rotation to radians
      rad = this._rotation*Math.PI/180;
      // get x and у components of thrust
      this.thrustX = Math.cos(rad)*thrust;
      this.thrustY = Math.sin(rad)*thrust;
      // add thrust to velocity
      this.velX += this.thrustX;
      this.velY += this.thrustY;
    }
    // add velocity to position
    this._x += this.velX;
    this._y += this.velY;
    // perform screen wrapping if (this._x>RIGHT) { this._x = LEFT;
    if (this._x<LEFT) {
      this._x =   RIGHT;
    }
    if   (this._y>BOTTOM) {
      this._y =   TOP;
    }
    if   (this._y<TOP) {
      this._y = BOTTOM;
    }
}
    Да, мы используем одну секцию за раз.
// rotate ship
if (rotate)   {
    this._rotation += rotate* 5;
}

Пример 8.1.

Довольно просто. Берем переменную поворота, которая может иметь значения -1 или +1 в зависимости от того, какая клавиша была нажата, или 0, если клавиша не была нажата. Умножаем ее на 5, чтобы ее значениями стали -5, 0 или +5? и добавляем результат к повороту корабля. 5 - просто число, хорошо подходящее по результатам тестирования. Вы можете настраивать это значение по вашему вкусу. В идеале нужно было бы записывать его в другую константу и определять его в функции init, например, ROTATESPEED = 5. Я просто выделил это здесь, чтобы сохранять функцию init как можно более простой.

Далее следует самая сложная часть функции move.

// move ship
if (thrust) {
    // convert rotation to radians
    rad = this._rotation*Math.PI/180;
    // get x and у components of thrust
    this.thrustX = Math.cos(rad)*thrust;
    this.thrustY = Math.sin(rad)*thrust;
    // add thrust to velocity
    this.velX += this.thrustX;
    this.velY += this.thrustY;
}

Если thrust равна 0 (нажата клавиша UP), этот фрагмент будет полностью пропущен. Если переменная имеет какое-то значение, этот код выполняется. Сначала выполняется преобразование поворота корабля (в градусах) в радианы. Затем берется значение thrust, которое соответствует углу наклона корабля, и раскладывается на компоненты X и Y - thrustX и thrustY - с использованием основ тригонометрии, изученных ранее в данной лекции. Рисунок показывает, какие действия выполняются.

После этого мы просто прибавляем значения ускорения к скоростям по направлению осей X и Y. Это дает новую скорость, с которой корабль будет двигаться после применения ускорения в этом направлении. Имейте в виду, что на рисунке выше, если бы корабль двигался в обратную сторону, и вы применили ускорение, оно было бы направлено в обратную сторону от направления движения корабля, поэтому корабль замедлил бы ход, остановился и начал движение в противоположном направлении - в точности, как мы хотели.

Последний фрагмент довольно прост. Здесь текущая скорость по направлению складывается с текущей позицией корабля, и если последний вышел за любую из границ рабочего места, он появляется на противоположной стороне.

// add velocity to position
this._x += this.velX;
this._y += this.velY;
// perform screen wrapping
if   (this._x>RIGHT) {
this._x =   LEFT;
}
if   (this._x<LEFT) {
    this._x = RIGHT;
}
if (this._y>BOTTOM) {
    this._y = TOP;
}
if   (this._y<TOP) {
    this._y = BOTTOM;
}
}

Настал волнующий момент. Сейчас вы запустите фильм, в котором реализованы все функциональности корабля. (В одном из углов будут находиться ненужные астероиды - не обращайте сейчас на них внимание!) Вы можете использовать три клавиши со стрелками для вращения и ускорения корабля на экране. Это очень похоже на оригинальную игру Asteroids, однако вы можете любым нужным вам образом настраивать переменные поворота и ускорения, чтобы достичь желаемого результата.

Теперь разберемся с "ленивыми" астероидами. Вот функция astMove.
function astMove () {
    // add velocity to position
    this._x += this.velX;
    this._y += this.velY;
    // perform screen wrapping
    if   (this._x>RIGHT) {
      this._x =   LEFT;
    }   else if   (this._x<LEFT)   {
      this._x = RIGHT;
    }   else if   (this._y>BOTTOM) {
      this._y = TOP;
    }   else if   (this._y<TOP)   {
      this._y = BOTTOM;
    }
    // check hitTest against ship_mc
    if   (this.hitTest(ship_mc._x, ship_mc._y, true)) {
      //   if ship is not already dead, destroy it
      if   (!shipDead) {
        destroyShip();
        shipDead = true;
      }
    }
}

Первая часть функции не требует объяснения. Здесь просто складываются скорость по направлению и позиция и затем осуществляется перенос. После этого следует проверка на столкновение астероида с кораблем.

// check hitTest against ship_mc
if   (this.hitTest(ship_mc._x, ship_mc._y, true)) {
    //   if ship is not already dead, destroy it
    if   (!shipDead)   {
      destroyShip();
      shipDead = true;
    }
}

Этот фрагмент реализует hitTest для фильма с использованием shapeFlag=true. Как вы помните, этот метод имеет один недостаток - он будет проверять только точку _x, _y корабля, которая является центральной точкой. Поэтому нос или хвост корабля будут проходить сквозь астероид, и столкновения при этом происходить не будет. Мы могли бы использовать shapeFlag=false и осуществлять проверку по граничному прямоугольнику. Однако вследствие этого корабль время от времени уничтожался бы без столкновения с астероидом. Из двух вариантов второй раздражал бы игроков гораздо больше, чем первый. Мы не можем использовать обнаружение коллизий по расстоянию, так как фильмы имеют неправильную форму, отличную от идеального круга или квадрата. Здесь возникла бы та же самая проблема. Вы можете попытаться найти более разумное решение этой проблемы, однако, как показывает практика, это сильно усложняет программу. Поэтому, в случае с нашим примером, позволим себе не доводить его до идеального состояния.

Если происходит столкновение, выполняется функция destroyShip, которая, помимо всего прочего, удаляет корабль с рабочего места. Я выяснил, однако, при разработке этой программы, что даже после того, как корабль удален, координаты, отправленные в hitTest, в течение нескольких кадров будут продолжать вызывать столкновение. Поэтому я установил переменную shipDead на значение true при первом попадании и запустил эту переменную в качестве предпосылки запуска функции destroyShip. Это обеспечило выполнение данной функции только один раз для каждой коллизии.
Раз уж зашла речь о функции destroyShip ():
function destroyShip() {
    // remove ship
    removeMovieClip(ship_mc);
    // update how many lives are left
    livesLeft--;
    // if none, end game.
    if   (livesLeft<1)   {
      gotoAndStop(2);
    }   else   {
      // tell it to come back in two seconds
      restoreID = setInterval(restoreShip, 2000);
    }
}

Эта функция удаляет фильм с кораблем с рабочего места и уменьшает переменную livesLeft.

Если livesLeft равна нулю, переходим в кадр 2 фильма и остаемся в нем. Я добавил в кадр 2 текст "Game Over" и кнопку перезапуска, которая возвращает фильм обратно в кадр 1.

В противном случае у нас остался еще как минимум один корабль. Мы используем setInterval для того, чтобы программа сделала паузу длиной в две секунды (это 2000 миллисекунд в переводе на время Flash), и затем выполняем функцию restoreShip. Имейте в виду, что здесь мы сохраняем ID интервала в переменной restoreID. Мы хотим, чтобы restoreShip выполнялась только один раз после столкновения, поэтому нам необходимо удалять интервал после его действия.
Вернемся к restoreShip.
function restoreShip() {
    // reincarnate ship
    shiplnit();
    shipDead = false;
    // make sure this function doesn't run again
    clearInterval(restoreID);
}
Здесь все достаточно ясно. Запускаем shipInit для возврата корабля на рабочее место. Затем сбрасываем shipDead на значение "ложь", чтобы можно было уничтожить корабль заново, если он столкнется с другим астероидом. Наконец, мы сбрасываем интервал, чтобы не восстанавливать повторно корабль каждые две секунды (очень надоедает, поверьте).
Можно запустить игру. Астероиды теперь будут полнофункциональными объектами, так же, как и ваш корабль. Вы можете попытаться избегать их, или, если вы садист, врезайтесь в астероиды и уничтожайте корабли! Ну, конечно, в целях тестирования:
Я также добавил динамическое текстовое поле на рабочее место и присвоил ему переменную livesLeft, чтобы можно было иметь визуальное представление о моих "подвигах Гастелло".
Теперь астероиды могут безжалостно врезаться в ваши корабли. Настало время мести.
В начале мы определили, что при нажатии клавиши SPACE будет выполняться функция shoot (). Ознакомимся с ней.
function shoot() {
    //   if we have any ammo left...
    if   (numShots<5) {
      numShots++;
      // create one shot and make it move
      shot_mc =   shots_mc.attachMovie("shot",
         "s"+shotIndex, shotIndex++);
      shot_mc.onEnterFrame = shotMove;
      // convert ship's rotation to radians
      rad = ship_mc._rotation*Math.PI/180;
      // position shot at ship's nose
      shot_mc._x = ship_mc._x+10*Math.cos(rad);
      shot_mc._y = ship_mc._y+10 *Math.s in(rad);
      // determine shot's velocity, adding it to ship's velicity
      shot_mc.velX = 5 *Math.cos(rad)+ship_mc.velX;
      shot_mc.velY = 5*Math.sin(rad)+ship_mc.velY;
    }
}

Еще один кусок кода. Давайте опять разобьем его на части.

function shoot() {
    //   if we have any ammo left...
    if   (numShots<5) {
      numShots++;
      //   create one shot and make it move
      shot_mc = shots_mc.attachMovie("shot",
        "s"+shotIndex, shotIndex++);
      shot_mc.onEnterFrame = shotMove;
Мы будем ограничивать число выстрелов пятью на каждый залп. При желании вы можете изменить это значение. Мы используем переменную numShots для протоколирования числа активных выстрелов, увеличивая ее значение с каждым новым выстрелом. По достижении значения 5, вся функция будет пропускаться. Если значение меньше пяти, будет добавляться фильм со снарядом в shots_mc (имейте в виду, что все выстрелы будут располагаться здесь для предотвращения конфликтов с астероидами по глубине). Мы присваиваем ссылку на этот фильм временной переменной shot_mc, а также присваиваем ее управляющий элемент onEnterFrame.
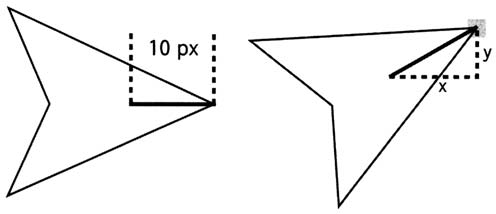
Нам нужно, чтобы снаряд вылетал не из центра корабля, а из его носа. Поэтому нам нужно выяснить координаты носа корабля. Рассмотрим следующий рисунок.

Мой корабль имеет 20 пикселей в ширину, а также центральную точку регистрации. Это означает, что от носа до центра 10 пикселей. При повороте корабля это расстояние также рано 10 пикселям, но, как видно из правого рисунка, мы имеем очень знакомый нам треугольник. Имея угол поворота и расстояние в 10 пикселей, мы можем выяснить значения x и y, как показано на рисунке.

x = cos(angle) * distance
y = sin(angle) * distance

Если прибавим их к значениям позиций _x и _y, то получим точную позицию для выстрела. Вот соответствующий ActionScript.

// convert ship's rotation to radians
rad = ship_mc._rotation*Math.PI/180;
// position shot at ship's nose
shot_mc._x = ship_mc._x + (10 * Math.cos(rad));
shot_mc._y = ship_mc._y + (10 * Math.sin (rad));

Теперь мы сделаем почти в точности то же самое для определения скорости выстрела по направлению. Я пришел к тому, что 5 - оптимальная скорость выстрела. Снаряд вылетит из корабля под таким же углом, какой имеет в данный момент корабль. Поэтому его скорости по направлению X и Y могут быть разложены следующим образом.

x velocity = cos(angle) *velocity
y velocity = sin(angle) *velocity

Другим небольшим внесенным мной дополнением было сложение текущей скорости по направлению корабля со скоростью снаряда, которую мы только что нашли. Если вы едете в автомобиле со скоростью 50 км/ч и бросаете из окна мяч со скоростью 10 км/ч в направлении движения автомобиля, то скорость мяча относительно земли будет равна 60 км/ч (здесь мы затрагиваем теорию относительности Эйнштейна, т.е. ее версию, представленную во Flash).

// determine shot's velocity, adding it to ship's velicity
shot_mc.velX = 5 * Math.cos(rad) + ship_mc.velX;
shot_mc.velY = 5 * Math.sin(rad) + ship_mc.velY;
У нас на экране есть снаряд, и у него есть своя скорость по направлению. Нам нужно просто завершить функцию shotMove, и все будет готово! Однако эта функция довольно хитроумная. Она будет выполнять все действия по реализации движения каждого снаряда, проверяя на столкновение с астероидами, разламывая астероиды или удаляя их, а также протоколируя количество заработанных очков. Ух! Описание этой функции я буду излагать последовательно, не сваливая на вас сразу целую страницу кода.
Для начала разберем хотя бы это короткое движение.

function shotMove() {
    // add velocity to position
    this._x += this.velX;
    this._y += this.velY;
    // if shot is out of range, remove it
      if (this._x>RIGHT | | this._x<LEFT | |
        this._y>BOTTOM | | this._y<TOP) {
      removeMovieClip(this);
      // update shot count
      if (numShots>0) {
      numShots--;
      }
    }
}

Здесь мы будем реализовывать сложную задачу, которая будет заключаться в использовании скорости по направлению для обновления позиции. Это уже нам знакомо. Затем мы выясняем, "вылетел" ли снаряд за пределы рабочего места. Если это так, удаляем его. Помните, что мы используем переменную numShots для протоколирования числа активных снарядов. Поэтому каждый раз при удалении снаряда мы уменьшаем переменную numShots. Я также выяснил, что иногда numShots может принимать отрицательное значение, что закончится тем, что можно будет выпускать больше пяти снарядов, так как переменная была уменьшена. Следовательно, прежде, чем уменьшать значение переменной, необходимо убедиться в том, что ее значение не равно нулю.

Сейчас вы можете запустить фильм. Снаряды уже выпускаются. Однако вскоре вы заметите, что снаряды кончились, и уничтожать астероиды уже не так легко.
Будем обрабатывать циклом массив, содержащий ссылки на все наши фильмы с астероидами, а также проверять коллизии для каждого из них.
function shotMove() {
    // add veloicty to position
    this._x += this.velX;
    this._y += this.velY;
    // if shot is out of range, remove it
    if (this._x>RIGHT | | this._x<LEFT | |
       this._y>BOTTOM | | this._y<TOP) {
      removeMovieClip(this);
      // update shot count if (numShots>0) {
        numShots--;
      }
    }
    // loop through asteroid array, checking for hit
    for (i=0; i<ast_array.length; i++) {
      if (ast_array[i].hitTest(this._x, this._y, true)) {
        // remove shot and update count removeMovieClip(this);
        if (numShots>0) {
          numShots--;
        }
        // remove asteroid from stage
        removeMovieClip(ast_array[i]);
        // and remove it from the array
        ast_array.splice(i, 1);
        // if this was the last one, create some new ones
        if (ast_array.length<1) {
          maxAst++;
          astInitID = setInterval(astInit, 2000);
        }
      }
    }
}

Мы используем ast_array.length в качестве управляющего элемента цикла for, так как он будет содержать число астероидов в массиве. Мы проверяем параметры снаряда _x и _y с использованием shapeFlag=true.

При попадании мы удаляем снаряд аналогично тому, как описано выше. После этого удаляем фильм с астероидом с рабочего стола и используем ast_array.spice(i, 1) для удаления этого элемента из массива. Имейте в виду, что это также уменьшит на единицу ast_array.length, что позволит нам всегда обрабатывать циклом точное число имеющихся астероидов.

Наконец, если ast_array достигает нуля - все астероиды успешно уничтожены - мы увеличиваем значение maxAst и создаем новую группу астероидов с помощью astInit. Однако мы добавим небольшой двухсекундный интервал перед запуском этой функции с помощью setInterval. Нам также потребуется удалять этот интервал astInitID, поэтому переходим к astInit и добавляем в него строку clearInterval.

function astInit() {
    // create a number of asteroids
    astIndex = 0;
    while (astIndex<maxAst) {
      createAst();
    }
    clearInterval(astInitID);
}

Теперь запустите проект и убедитесь, что все работает. Вы должны иметь возможность уничтожить три астероида, после чего должны появиться четыре астероида, а после их уничтожения появятся пять "камушков". Итак, атака отбита, и теперь корабль имеет большое преимущество над этими космическими скалами. Давайте сделаем астероиды более опасными.
Вместо исчезновения после единственного попадания снаряда, давайте сделаем так, чтобы астероиды раскалывались на части, как в игре Atari Asteroids. Сначала нам нужно, чтобы на месте попадания снаряда появлялось два астероида. Мы реализуем это с помощью функции createAst. Затем нам нужно будет сделать их меньшими, нежели исходный астероид. Это делается посредством изменения размеров фильмов.
фильмов.
function shotMove() {
    // add veloicty to position
    this._x += this.velX;
    this._y += this.velY;
    // if shot is out of range, remove it
    if (this._x>RIGHT | | this._x<LEFT | | this._y>BOTTOM | | this._y<TOP) {
      removeMovieClip(this);
      // update shot count
      if (numShots>0) {
        numShots--;
      }
    }
    // loop through asteroid array, checking for hit
    for (i=0; i<ast_array.length; i++) {
      if (ast_array[i].hitTest(this._x, this._y, true)) {
        // remove shot and update count
        removeMovieClip(this);
        if (numShots>0) {
          numShots--;
        }
        // if asteroid is big enough, break it in two
        if (ast_array[i]._xscale>25) {
          // make this asteroid 1/2 size
          ast_array[i]._xscale /= 2;
          ast_array[i]._yscale /= 2;
          // create a new asteroid, make it same size, same position
          ast_mc = createAst();
          ast_mc._xscale = ast_array[i]._xscale;
          ast_mc._yscale = ast_array[i]._yscale;
          ast_mc._x = ast_array[i]._x;
          ast_mc._y = ast_array[i]._y;
        } else {
          // if asteroid is small, remove it from the stage
          removeMovieClip(ast_array[i]);
          // and remove it from the array
          ast_array.splice(i, 1);
          // if this was the last one, create some new ones
          if (ast_array.length<1) {
            maxAst++;
            astlnitID = setlnterval(astlnit, 2000);
          }
        }
      }
    }
}

Пример 8.2.

Первой частью этого кода является

if (ast_array[i]._xscale>25) {
    // make this asteroid 1/2 size
    ast_array[i]._xscale /= 2;
    ast_array[i]._yscale /= 2;

Сначала проверяем _xscale астероида, в который попал снаряд. Если это значение больше 25, делим его на два. Его начальной величиной будет 100. После первого попадания значением станет 50. Попадание второго снаряда уменьшит размер до значения 25. После этого выражение if примет значение "ложь", и выполнится выражение else, код которого удалит астероид.

Мы сделали имеющийся фильм меньше, и нам нужно добавить еще один, сделать его такого же размера и поместить его на той же позиции, что и первый. Это будет реализовывать вторая половина блока if.

// create a new asteroid, make it same size, same position
ast_mc = createAst();
ast_mc._xscale = ast_array[i]._xscale;
ast_mc._yscale = ast_array[i]._yscale;
ast_mc._x = ast_array[i]._x;
ast_mc._y = ast_array[i]._y;

Помните, что функция createAst возвращает ссылку на созданный астероид. Здесь-то мы ее и используем. Мы присваиваем ее временной переменной ast_mc и настраиваем ее параметры _xscale, _yscale, _x и _y таким образом, чтобы они совпадали с параметрами астероида, в который только что попал снаряд. Также запомните, что createAst присваивает каждому новому астероиду случайные скорость и поворот, поэтому эти два маленьких обломка будут разлетаться различным образом в разных направлениях.

Другим действием, которое выполняется createAst, является добавление нового астероида в массив ast_array, чтобы он в будущем проверялся автоматически при последующих проверках элементов массива на попадание. Сейчас все функциональности собираются воедино.

Последнее, но не менее важное: нам нужно обеспечить подсчет очков. Я разместил еще одно динамическое текстовое поле вверху рабочего места для отображения количества очков. После этого добавляем последний штрих в нашу функцию shotMove. Теперь будет выполняться операция переключения на основе значения _xscale астероида, в который только что попал снаряд, и присваиваться разное количество очков, в зависимости от размера астероида - 100, 50 или 25. Это количество прибавляется к текущей сумме очков в поле.

function shotMove() {
    // add velocity to position
    this._x += this.velX;
    this._y += this.velY;
    // if shot is out of range, remove it
    if (this._x>RIGHT | | this._x<LEFT | | this._y>BOTTOM | | this._y<TOP) {
      removeMovieClip(this);
      // update shot count
      if (numShots>0) {
        numShots--;
      }
    }
    // loop through asteroid array, checking
    for hit for (i=0; i<ast_array.length; i++) {
      if (ast_array[i].hitTest(this._x, this._y, true)) {
        // determine score based on asteroid's size (_xscale)
        switch (ast_array[i]._xscale) {
        case 100 :
          score += 10;
          break;
        case 50 :
          score += 50;
            break;
          case 25 :
            score += 100;
            break;
          }
          // remove shot and update count
          removeMovieClip(this);
          if (numShots>0) {
            numShots--;
        }
        // if asteroid is big enough, break it in two
        if (ast_array[i] ._xscale>25) {
          // make this asteroid 1/2 size
          ast_array[i] ._xscale /= 2;
          ast_array[i] ._yscale /= 2;
          // create a new asteroid, make it same size, same position
          ast_mc = createAst();
          ast_mc._xscale = ast_array[i] ._xscale;
          ast_mc._yscale = ast_array[i] ._yscale;
          ast_mc._x = ast_array[i] ._x;
          ast_mc._y = ast_array[i] ._y; }
        else {
          // if asteroid is amall, remove it from the stage
          removeMovieClip (ast_array[i]);
          // and remove it from the array
          ast_array.splice(i, 1);
          // if this was the last one, create some new ones
          if (ast_array.length<1) {
            maxAst++;
            astlnitID = setInterval(astlnit, 2000);
          }
        }
      }
    }
}

Пример 8.3.

Итак, мы получили полнофункциональную версию игры Asteroids а-ля Flash, которая, однако, имеет огромное поле деятельности для усовершенствования и изменения. Вы можете сделать так, чтобы корабль взрывался при столкновении с астероидом. Это можно реализовать с помощью построения промежуточного объекта, начинающегося с третьего кадра корабля. Нужно просто выполнить gotoAndPlay(3) при попадании астероида перед его удалением. Вы можете захотеть добавить звуки с использованием материала, изученного в других местах этой книги. Вы также можете сделать так, чтобы, как и в оригинальной игре, появлялся вражеский корабль, что сделает бой еще более интересным и сложным. Для этого может быть использована большая часть того, что мы делали в нашей предыдущей "стрелялке".

Все эти возможности внесут свои собственные сложности и небольшие проблемы, по мере добавления их в текущую игру, однако надеемся, что вы уже достаточно разбираетесь в материале, и ваших знаний хватит, чтобы разрешить возникшие трудности.

Теперь давайте изучим некоторые физические свойства Flash.

Пружинящие объекты

В двух последних примерах мы имели дело с реалистичным движением объектов. Они отскакивали от стен и пола, падали вниз с реалистичной гравитацией и ускоряли свое движение в космическом пространстве. Существует еще один тип движения, о котором я хотел бы рассказать: пружинящее движение, часто связываемое с понятием эластичности.

Я знаю, что вы сомневаетесь в широком применении данного типа движения, но как только вы поймете его суть, вы найдете пружинящим объектам очень много применений в самых различных местах. Эффект пружины можно интерпретировать как вид ускорения. Представьте, что у вас есть объект на одном конце пружины, а дугой ее конец закреплен на фиксированной точке. Если отпустить объект, пружина заставит его ускоряться по направлению к фиксированной точке. Это очень похоже на гравитационные силы, увлекающие объект вниз, или на ускоритель ракеты, действующий в определенном направлении.

О пружинящих объектах необходимо знать две очень важные вещи.

Пружина, как правило, ускоряется по направлению к определенной точке. Если она пройдет эту точку, ее движение замедлится, направление движения поменяется, и начнется ускорение в обратную сторону по направлению к той же точке.
Ускорение пропорционально расстоянию между объектом и конечной точкой.

Иными словами, второй пункт означает, что чем дальше объект находится от точки закрепления пружины, тем большая ускоряющая сила действует на него по направлению к этой точке. Мысленно вы об этом догадываетесь. Если бы я держал один конец одежной резинки напротив вашей руки, находящейся рядом с точкой закрепления, и оттянул бы ее на несколько сантиметров, вы посмотрели бы на меня вопросительно, так как вы догадывались бы, что отпусти я резинку, она бы отскочила с небольшой силой. Однако, если бы я оттянул ее назад со всей своей силой, вы бы убрали руку от греха подальше. Если бы я отпустил резинку в этот момент, она получила бы очень большое ускорение и могла бы причинить вам боль.

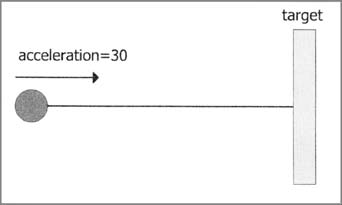
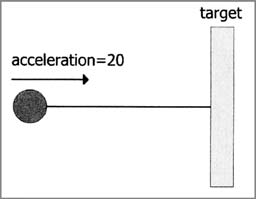
Теперь рассмотрим некоторые иллюстрации. На первом рисунке показана воображаемая пружина, полностью оттянутая назад. Ускорение максимально и равно, скажем, +30.

Представьте себе эту ситуацию во Flash: объект начинает двигаться со скоростью 30 пикселей в кадр. В следующем кадре объект становится несколько ближе к цели и пружина уже натянута чуть слабее. Она добавляет ускорение, скажем, равное 20. Итак, теперь объект двигается со скоростью 50 пикселей в кадр. Этот принцип очень важно понимать. Объект не замедляется, а все еще ускоряется - т.е. продолжает увеличивать скорость - но увеличение его скорости не постоянно во времени.

В следующем кадре объект уже находится довольно близко к цели. На него действует совсем небольшое ускорение, быть может, равное 3. Из этого следует, что его скорость в итоге стала равной 53. Имейте в виду, что его скорость не уменьшается; становится меньшей величина ускорения. Скорость объекта выше, чем в предыдущем кадре.

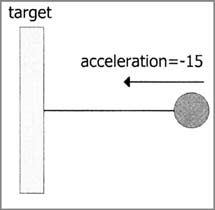
Перейдем к следующему кадру. Объект движется так быстро, что "вылетает" за пределы конечной точки, наподобие собаки, гоняющейся за мячиком по льду. Теперь цель находится "за" объектом. Сейчас пружина будет действовать на объект с силой, обеспечивающей обратное ускорение объекта. Когда объект будет находиться достаточно далеко по другую сторону от конечной точки, ускорение, очевидно, будет довольно сильным, достаточным для остановки объекта. Предположим, на объект действует ускорение величиной -15. Наш объект все еще движется, однако его скорость уменьшается до значения 38.

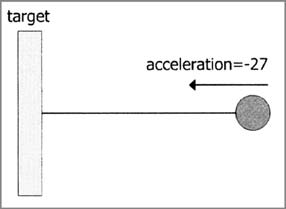
Сейчас, чем дальше объект находится от точки закрепления пружины, тем ее "возвращающее" действие будет сильнее. Ускорение равно -27, что замедляет объект до скорости 11. В следующем кадре ускорение будет достаточно велико для того, чтобы преодолеть ту небольшую остаточную скорость, которую имеет объект, после чего начнется движения в противоположную сторону.

Итак, нужно перевести эту теорию на язык ActionScript. Давайте воссоздадим это пружинящее движение во Flash.

Пружина

Откройте новый основной фильм и создайте в нем новый клип. Как обычно, я создал шарик с именем инстанса ball_mc. В середине экрана (275, y) нарисуйте простую линию. Она будет играть роль графического представления конечной точки, на которой будет базироваться наше пружинящее движение.
Добавьте новый слой с именем actions и в кадре 1 объявите переменную для представления нашей конечной точки (в этом упражнении мы используем разрешение по осям).
var centerX = 275;
Теперь нам нужно определить "пружинящий" множитель или, говоря более определенно, насколько сильное ускорение будет действовать на объект на каждом расстоянии. Он будет выражен в виде дроби. По существу, мы будем брать отношение расстояния между объектом и точкой закрепления пружины и использовать его в качестве значения ускорения. Нам подойдут значения около 0,2. Oднако вы можете поэкспериментировать с различными величинами, чтобы достичь желаемого результата. Этот множитель обычно обозначается k. Это не очень информативно, однако, если использовать его всегда, вы будете понимать, что означает k. Итак, вот наш файл.
var centerX = 275;
var k = .2;
Мы настроили рабочее место, и можно приступать к реализации действия. Сначала необходимо определить расстояние по одному измерению - вычесть ball_mc._x из centerX. После этого умножаем расстояние на k, чтобы получить значение ускорения, которое будет записано в переменную accX. Затем прибавляем accX к нашей скорости velX и, наконец, прибавляем скорость к ball_mc._x. Мы реализуем эти сложения под двумя имеющимися строками в функции onEnterFrame.
onEnterFrame = function () {
    dx = centerX-ball_mc._x;
    accX = dx*k;
    velX += accX;
    ball_mc._x += velX;
};

Здесь я выделил для ясности каждый из шагов. Некоторые предпочитают выполнять все шаги сложной функции в одной строке следующим образом.

ball_mc._x += velX += (centerX-ball_mc._x)*k;

Так можно делать, но такое выражение довольно сложно прочесть. Вы можете ввести свой собственный способ записи функции и сжать ее так, как вам нужно.
Если сейчас запустить фильм, на экране появится "красиво" пружинящий около точки закрепления объект. Но есть одна проблема: мы реализовали идеальный случай, в котором отсутствуют силы трения и всякая потеря энергии, поэтому наш объект будет совершать пружинящие колебания вечно. Давайте добавим некоторое трение, аналогично тому, как мы это сделали в примере с "бросанием" объекта в лекции 6. Мы будем просто умножать скорость на дробь вроде 0,9 в каждом кадре. Благодаря этому колебание объекта будет замедляться, что сделает данный пример более реалистичным. Просто добавьте следующую строку.
var centerX = 275;
var k = .2;
onEnterFrame - function () {
    dx = centerX-ball_mc._x;
    accX = dx*k;
    velX += accX;
    velX *= .9;
    ball_mc._x += velX;
};
Запустите фильм и вы получите довольно реалистичное пружинящее движение.
Можно легко продолжить работу и изменить этот файл так, что пружинящее движение будет осуществляться по осям x и y. Я реализовал это и сделал ball_mc перетаскиваемым в исходном файле Spring_2_dimensions.fla, на случай, если вы решите заняться дальнейшим экспериментированием. Весь код обсуждался ранее, поэтому я не буду останавливаться на этом файле. Если вы запустите его, вы сможете "зацеплять" и "бросать" мячик, и он всегда, в конечном счете, будет возвращаться в центр экрана.

Я советую вам продолжить дальнейшее изучение этой области. С помощью этих простейших принципов можно достичь очень многих результатов, необходимо только как следует разобраться в них. Вот некоторые идеи для экспериментирования.

Вместо фиксированной конечной точки (centerX, centerY), сделайте конечную точку перемещаемой. Попробуйте использовать (this._xmouse, this._ymouse) для определения положения точки.
Вы можете создать другой перетаскиваемый фильм с именем anchor_mc. Заставьте шарик пружинить по направлению к точке (anchor_mc._x, anchor_mc._y).
Чтобы отобразить графически само колебание, добавьте следующий код в конец функции spring, после перемещения ball на новую позицию.
clear();
lineStyle(1, 0, 100);
moveTo(centerX, centerY);
lineTo(ball_mc._x, ball_mc._y);
Наконец, добавьте гравитацию! Не существует причин, по которым на ваш объект не может действовать несколько сил ускорения. Просто добавьте в файл строку velY += grav; а перед этим укажите значение для grav. Вы увидите, что вам потребуется указать гораздо большее значение гравитации, нежели в предыдущих примерах. С другой стороны, можно немного уменьшить коэффициент k.

Мы изучили большое количество материала, с помощью которого были реализованы несложные, но красивые эффекты. Однако у меня есть еще пара стоящих примеров, которые хотелось бы вам показать. Я догадываюсь, что вы сейчас хотите поэкспериментировать с пружинящими объектами. Когда закончите, продолжайте читать дальше - мы вернемся к тригонометрии и продолжим ее использовать для достижения интересных эффектов.

Поворот координат

До этого момента мы постоянно поворачивали точки, линии и векторы. В основном, мы начинали с радиуса от фиксированной точки и затем поворачивали его на определенный угол. Это способ довольно эффективен, однако вспомните, что когда мы рисовали наш корабль или стрелку, нужно было, чтобы они "смотрели" вправо (0 градусов), так как все повороты основывались на вращении чего-либо, начиная с нулевого угла.

Что будет, если поворачивать объект вокруг центральной точки на определенное количество градусов, а этот объект находится под углом, отличным от нулевого? Как быть в случае, если нам известны лишь координаты x и y объекта, а мы хотим вращать его вокруг центральной точки? Давайте рассмотрим следующий случай.

Здесь мы наблюдаем объект, расположенный на координате x=100 и на 120 пикселей выше центральной точки. Теперь предположим, что нам нужно повернуть объект на 20 градусов вокруг центральной точки. Возникает проблема, заключающаяся в том, что объект не находится под углом ноль градусов, с которого можно начать вращение. Можно было бы использовать теорему Пифагора для вычисления расстояния от центра, значение atan2 для выяснения текущего угла объекта, и затем прибавить 20 градусов к этому значению и с помощью sin и cos выяснить новые значения X и Y.

Однако это слишком длинный способ, и можно сделать это гораздо быстрее, особенно в случае с множеством объектов. Сейчас я отклонюсь от привычного способа изложения и приведу формулы без объяснения того, как они были получены. Здесь просто утверждается, что данные формулы работают, поэтому просто запомните их для дальнейшего использования.

Когда нужно повернуть точку (x, y) на определенный угол (angle), нужно использовать следующие выражения.

new_x = x*cos (angle) - y*sin (angle)
new_y = y*cos (angle) + x*sin (angle)

Я записал это на клочке бумаги и прикрепил на стенку рядом с моим компьютером. Теперь я уже запомнил эти выражения довольно четко.

Заметка: процесс вывода этих формул не является секретной информацией. Это стандартная операция, используемая при повороте координат. Если вам интересно их получение, вы можете найти его в любой книге по тригонометрии и изучить их вывод. Я не рассказываю здесь об этом по той причине, что это выходит за рамки рассматриваемой тригонометрии, применимой к Flash.

На следующем рисунке изображены связи между x, y и new_x, new_y, а также угол, на который мы поворачиваем объект.

Попробуем применить это на деле во Flash.

Полет кораблей

Откройте фильм из предыдущего упражнения этой лекции. Вам понадобится лишь фильм в вашей библиотеке Library, который мы сможем использовать в виде объектов для вращения. Добавьте три копии фильма в любые позиции на рабочем столе и назовите их инстансы именами mc1_mc, mc2_mc и mc3_mc. Мы будем вращать их вокруг центра рабочего места, поэтому нарисуйте рисунок в точке (275, 200), который будет играть роль центральной точки. Я изобразил в центре планету Земля, по орбите которой и будут "летать" корабли:
Теперь добавьте новый слой с именем actions и введите следующий код в кадре 1.
init();
function init() {
    cx = 275;
    cy = 200;
    onEnterFrame = rotate;
    var angle = 2;
    rad = angle*Math.PI/180;
    cosAngle = Math.cos(rad);
    sinAngle = Math.sin(rad);
}

Рассмотрим этот код. Функция init будет указывать центральную точку и настраивать функцию onEnterFrame. После этого будет устанавливаться angle для поворота объектов в каждом кадре, с последующим переводом в радианы. Следующие две строки не добавляют ничего в функциональность программы. Однако они обеспечивают должную эффективность. Так как нам понадобится использовать cos и sin угла дважды в каждом кадре фильма, и так как они никогда не изменяются, не имеет смысл вычислять их 30 или 40 раз в секунду! Это будет делаться лишь один раз в начале фильма, с сохранением значений в переменных cosAngle и sinAngle, после чего эти переменные будут использоваться повсеместно в оставшейся части фильма.
Теперь мы создадим функцию rotate. Она будет циклически обрабатывать три фильма и применять формулу поворота координат к их позициям.
function rotate() {
    for (i=1; i<4; i++) {
      x = this["mc"+i+"_mc"]._x-cx;
      у = this["mc"+i+"_mc"]._y-cy;
      x1 = x*cosAngle-y*sinAngle;
      y1 = y*cosAngle+x*sinAngle;
      this["mc"+i+"_mc"]._x = x1+cx;
      this["mc"+i+"_mc"]._y = y1+cy;
    }
}

Помните, что всегда необходимо определять, вокруг чего осуществлять вращение - т.е. центральную точку - и в вычислениях отталкиваться именно от этой точки. mc1_mc расположен в точке (375,y), на расстоянии 100 пикселей от центральной точки, и 375 - то значение X, которое мы используем в вычислениях. Следовательно, мы будем вычитать значения центральной точки cx и cy из текущих координат каждого фильма. После этого будет выполняться поворот с присвоением результатов x1 и y1. Это даст новую позицию фильма относительно центральной точки, поэтому нужно прибавить cx и cy для определения наших конечных координат.
В качестве последнего небольшого дополнения, добавим несколько функций, рисующих линии, для визуализации вращения. Приведем окончательный код программы.
init();
function init() {
    cx = 275;
    cy = 200;
    onEnterFrame = rotate;
    var angle = 2;
    rad = angle*Math.PI/180;
    cosAngle = Math.cos(rad);
    sinAngle = Math.sin(rad);
}
function rotate() {
    for (i=1; i<4; i++) {
      x = this["mc"+i+"_mc"]._x-cx;
      у = this["mc"+i+"_mc"]._y-cy;
      x1 = x*cosAngle-y*sinAngle;
      y1 = y*cosAngle+x*sinAngle;
      this["mc"+i+"_mc"]._x = x1+cx;
      this["mc"+i+"_mc"]._y = y1+cy;
      clear ();
      lineStyle (1, 0, 80);
      moveTo (mc1_mc._x, mc1_mc._y);
      lineTo (mc2_mc._x, mc2_mc._y);
      lineTo (mc3_mc._x, mc3_mc._y);
      lineTo (me1_mc._x, mc1_mc._y);
      moveTo(cx, cy);
      lineTo (mc1_mc._x, mc1_mc._y);
      moveTo (cx, cy);
      lineTo (mc2_mc._x, mc2_mc._y);
      moveTo (cx, cy);
      lineTo (mc3_mc._x, mc3_mc._y);
    }
}

Пример 8.4.
Запустите фильм. Вы увидите три фильма, поворачивающиеся вокруг центральной точки. Если вы хотите сравнить ваш файл с моим, вы можете использовать coordinate_rotation.fla в исходных файлах.

Проект №2: Bounce

Наш последний проект будет включать в себя практически весь спектр рассмотренного до сих пор материала. Мы не будем рассматривать другие новые концепции, а будем комбинировать уже реализованные идеи для достижения некоторых совершенно новых эффектов. С помощью материала, изученного в последних лекциях, вы можете создавать бесчисленное количество интересных эффектов. Нужно просто искать новые способы применения принципов программирования и их различных комбинаций. Разумеется, все, что вы узнаете с этого момента, будет только преумножать ваши знания по мере того, как вы будете пытаться комбинировать новое с уже изученным материалом. Итак, приступим.

До сих пор мы рассматривали объекты, отскакивающие от прямых "стен", "полов" и "потолков". Но что будет, если стена не прямая? Предположим, что шарик движется под углом 57 градусов и ударяется о стену, наклоненную под углом 32 градуса. Под каким углом и с какой скоростью в этом случае он отскочит? Сейчас у нас есть все средства для выяснения этого. Рассмотрим следующий рисунок.

Шарик движется под определенным углом, ударяется о стенку и отскакивает под показанным углом. Теперь, перед тем, как расстраиваться из-за того, что это может оказаться очень трудным для понимания, обратимся к следующему рисунку.

Это несложный случай, не так ли? Ничуть не сложнее того, что мы реализовали в игре "pong". Здесь просто осуществляется проверка того, находится ли шарик ниже уровня пола, и обращается в отрицательную скорость по направлению Y. Два этих рисунка по сути представляют собой одно и тоже. Я просто повернул второй из них, чтобы сделать пол расположенным горизонтально. Стратегия такова: мы поворачиваем всю конструкцию, чтобы реализовать действие для случая с плоским полом, выполняем действия для отскакивания шарика, затем поворачиваем все обратно. На самом деле нам нужно поворачивать не только координаты X и Y шарика, но также его скорости X и Y (представлены первой стрелкой на рисунке). (Это файл chapter8-final.fla на компакт-диске).

Сначала нарисуем стену. Это будет просто прямая горизонтальная линия в фильме, с именем инстанса wall_mc, и создадим шарик с именем ball_mc.
Повернем стену вручную, но не больше, чем на +90 или -90 градусов.
Теперь давайте создадим функцию init, которая будет обеспечивать гравитацию, отскакивание шарика, определять функцию onEnterFrame, а также сделаем наш шарик перетаскиваемым и бросаемым.
init();
function init() {
    // set some constants
    grav = .5;
    bounce = -.8;
    TOP = 0;
    BOTTOM = Stage.height;
    LEFT = 0;
    RIGHT = Stage.width;
    // our animation function
    onEnterFrame = move;
    // make the ball draggable
    ball_mc.onPress = function() {
      this.startDrag();
      this.dragging = true;
    };
    ball_mc.onRelease = ball_mc.onReleaseOutside=function() {
      this.stopDrag();
      this.dragging = false;
    };
}
После этого мы определим нашу главную функцию move, без проверки коллизий.
function move() {
    // if we are not dragging the ball
    if (!ball_mc.dragging) {
      // add gravity to the у velocity
      ball_mc.velY += grav;
      // add velocity to the position
      ball_mc._x += ball_mc.velX;
      ball_mc._y += ball_mc.velY;
      // if ball hits any wall, position it at the edge of the wall
      // and have it bounce
      if (ball_mc._x<LEFT+ball_mc._width/2) {
        ball_mc._x = LEFT+ball_mc._width/2;
        ball_mc.velX *= bounce;
      } else if (ball_mc._x>RIGHT-ball_mc._width/2) {
        ball_mc._x = RIGHT-ball_mc._width/2;
        ball_mc.velX *= bounce;
      } else if (ball_mc._y<OP+ball_mc._height/2) {
        ball_mc._y = TOP+ball_mc._height/2;
        ball_mc.velY *= bounce;
      } else if (ball_mc._y>BOTTOM-ball_mc.__height/2) {
        ball_mc._y = BOTTOM-ball_mc._height/2;
        ball_mc.velY *= bounce;
      }
    } else {
      // if we ARE dragging the ball
      // velocity = new position - old position
      ball_mc.velX = ball_mc._x-ball_mc.oldx;
      ball_mc.velY = ball_mc._y-ball_mc.oldy;
      // reset old position for next time
      ball_mc.oldx = ball_mc._x;
      ball_mc.oldy = ball_mc._y;
    }
}

Пример 8.5.

Здесь содержится довольно большое количество кода, однако он уже весь вам знаком.
Так как наш код обеспечения проверки столкновений и отскакивания шарика будет довольно сложным, мы переместим его в его собственную функцию. Вставьте эту строку сразу после определения параметров _x и _y фильма ball_mc.
checkWall (wall_mc);

Теперь приступим к определению этой функции. Перед тем, как погружаться в математику, добавим код для обеспечения уверенности в том, что шарик находится поблизости с помощью простой проверки hitTest.
function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
    ...
    }
}
Установив shapeFlag на значение "ложь", мы используем только граничный прямоугольник стены. Если шарик не находится внутри этой области, функция просто не выполнится. В противном случае, переходим к следующему шагу.
В hitTest мы сначала определяем начальные значения X и Y посредством вычитания координат wall из координат ball. После этого преобразуем угол поворота _rotation (в градусах) объекта wall в радианы и устанавливаем переменные cosAngle и sinAngle. Все это проделывалось в предыдущем файле.
function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
      // if so, determine ball's x and у position
        in relation to the wall
      x = ball_mc._x-wall_mc._x;
      у = ball_mc._y-wall_mc._y;
      // convert wall's angle to radians and
         compute cos and sin of it
      rad = wall_mc._rotation*Math.PI/180;
      cosAngle = Math.cos(rad);
      sinAngle = Math.sin(rad);
    }
}
Теперь я расскажу о небольшой альтернативе нашим предыдущим формулам поворота координат. (Я говорил о том, что здесь не будет ничего нового, однако это всего лишь небольшое изменение!) Приведенные мной формулы прибавляли угол к координатам. Другими словами, если бы вы прибавили 30 градусов, система координат повернулась бы в положительном направлении на 30 градусов. Однако в данном случае, предположим, что наша стена находится под углом 30 градусов, и нам нужно повернуть ее на -30 градусов, чтобы она стала горизонтальной. Конечно, можно было бы просто использовать в той же формуле значение -30 вместо +30, но так как мы заранее вычисляем значения sin и cos, этот способ является более эффективным. Формулами вычитания угла из системы координат являются следующие выражения.
new_x = cos (angle) *x + sin (angle) *y
new_y = cos (angle) *y - sin (angle) *x
Единственное отличие заключается в замене знаков + и - в середине выражений. Чтобы вычесть угол стены из координат шарика, нужно добавить следующие строки.
function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
      // if so, determine ball's x and у position
         in relation to the wall
      x = ball_mc._x-wall_mc._x;
      у = ball_mc._y-wall_mc._y;
      // convert wall's angle to radians and compute
         cos and sin of it
      rad = wall_mc._rotation*Math.PI/180;
      cosAngle = Math.cos(rad);
      sinAngle = Math.sin(rad);
      // rotate coordinates to align with wall angle
      x1 = cosAngle*x+sinAngle*y;
      y1 = cosAngle*y-sinAngle*x;
    }
}

Теперь нам нужно также реализовать поворот скоростей. Это можно интерпретировать как поворот стрелки на рисунке.

function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
      // if so, determine ball's x and у position
        in relation to the wall
      x = ball_mc._x-wall_mc._x;
      у = ball_mc._y-wall_mc._y;
      // convert wall's angle to radians and compute
         cos and sin of it
      rad = wall_mc._rotation*Math.PI/180;
      cosAngle = Math.cos(rad);
      sinAngle = Math.sin(rad);
      // rotate coordinates to align with wall angle
      x1 = cosAngle*x+sinAngle*y;
      y1 = cosAngle*y-sinAngle*x;
      // rotate velocities to align with wall angle
      vx1 = cosAngle*ball_mc.velX+sinAngle*ball_mc.velY;
      vy1 = cosAngle*ball_mc.velY+sinAngle*ball_mc.velX;
    }
}

Заметьте, что мы не поворачиваем ни один из текущих фильмов. Это было бы пустой тратой процессорного времени, так как мы в любом случае поворачивали бы их обратно перед тем, как кто-либо их заметил. Все наши вычисления здесь носят чисто математический характер. Мы имеем воображаемый горизонтальный пол, расположенный в точке (0,0), и воображаемый шарик, расположенный на координатах x1, y1 и двигающийся с воображаемой скоростью vx1, vy1. Все, что мы сделали, это реализовали математическое представление второго, повернутого рисунка.
Теперь нужно применить простой код для отскакивания шарика от горизонтального пола.
1. Выяснить, находится ли шарик ниже пола.
2. Если это так, переместить его на один уровень с полом.
3. Обратить его скорость по направлению Y.
Так как пол теоретически имеет координаты (0,0), для учета толщины шарика мы используем следующий код:

if (y1>0-ball_mc._height/2) {
. . .
}

Все так же, как было раньше.

if (ball_mc._y>BOTTOM-ball_mc._height/2){
. . .
}

Вместо этого мы просто используем координаты после поворота. Если это так - выходим из программы. В противном случае, мы настраиваем позицию шарика и обращаем его скорость по направлению Y. В терминах системы координат после поворота имеем следующее.

function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
      // if so, determine ball's x and у position
         in relation to the wall
      x = ball_mc._x-wall_mc._x;
      у = ball_mc._y-wall_mc._y;
      // convert wall's angle to radians and compute
         cos and sin of it
      rad = wall_mc._rotation*Math.PI/180;
      cosAngle = Math.cos(rad);
      sinAngle = Math.sin(rad);
      // rotate coordinates to align with wall angle
      x1 = cosAngle*x+sinAngle*y;
      y1 = cosAngle*y-sinAngle*x;
      // rotate velocities to align with wall angle
      vx1 = cosAngle*ball_mc.velX+sinAngle*ball_mc.velY;
      vy1 = cosAngle*ball_mc.velY+sinAngle*ball_mc.velX;
      // check if ball is hitting wall
      if (y1>0-ball_mc._height/2) {
        // do simple bounce calculation, adjusting position of
        Кball to align with the edge of wall
        y1 = 0-ball_mc._height/2;
        vy1 *= bounce;
      }
    }
}
Теперь выполняем обратный поворот посредством прибавления угла вместо вычитания, поэтому возвращаемся к исходной формуле. Это делается в последнем блоке if после vy1 *= bounce.
x = cosAngle*x1 - sinAngle*y1;
y = cosAngle*y1 + sinAngle*x1;
И скорости:
ball_mc.velX = cosAngle*vx1 - sinAngle*vy1;
ball_mc.velY = cosAngle*vy1 + sinAngle*vx1;
После этого мы обратно прибавляем x и y к значениям wall._x и wall._y для возврата в текущее положение для шарика на рабочем столе.
ball_mc._x = x+wall_mc._x;
ball_mc._y = y+wall_mc._y;

Если шарик сталкивается с линией, он располагается непосредственно на ней, и его скорость станет таковой, что он отскочит от линии под реалистичным углом. Приведем полный код функции checkWall.

function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
      // if so, determine ball's x and у position in relation to the wall
      x = ball_mc._x-wall_mc._x;
      у = ball_mc._y-wall_mc._y;
      // convert wall's angle to radians and compute cos and sin of it
      rad = wall_mc._rotation*Math.PI/180;
      cosAngle = Math.cos(rad);
      sinAngle = Math.sin(rad);
      // rotate coordinates to align with wall angle
      x1 = cosAngle*x+sinAngle*y;
      y1 = cosAngle*y-sinAngle*x;
      // rotate velocities to align with wall angle
      vx1 = cosAngle*ball_mc.velX+sinAngle*ball_mc.velY;
      vy1 = cosAngle*ball_mc.velY+sinAngle*ball_mc.velX;
      // check if ball is hitting wall
      if (y1>0-ball_mc._height/2) {
        // do simple bounce calculation, adjusting position of ball
        // to align with edge of wall
        y1 = 0-ball_mc._height/2;
        vy1 *= bounce;
        // rotate coordinates back to original angle
        x = cosAngle*x1-sinAngle*y1;
        у = cosAngle*y1+sinAngle*x1;
        // rotate velocities back to original angle
        ball_mc.velX = cosAngle*vx1-sinAngle*vy1;
        ball_mc.velY = cosAngle*vy1+sinAngle*vx1;
        // adjust wall-relative position to stage position
        ball_mc._x = x+wall_mc._x;
        ball_mc._y = y+wall_mc._y;
      }
    }
}

Пример 8.6.

Вы наверняка захотите увидеть эту функцию в действии, поэтому можете немного с ней поэкспериментировать.

Одним из моментов, с которым вы можете столкнуться - это то, что когда шарик приближается к обратной стороне стенки, он может неожиданно перескочить наверх. Это происходит потому, что мы проверяем, находится ли y1 просто под полом. Не имеет значения, на сколько именно ниже пола он находится. Мы можем обеспечить 99% уверенности в этом, добавив другое условие к выражению if. Мы знаем, что если шарик двигается вниз и проходит через стенку, самой дальней точной, которой он может достичь после стенки, является vy1, так как это наибольшее расстояние, на которое он может переместиться в одном кадре. Поэтому, если шарик находится дальше этой точки под стенкой, он должен был появиться со стороны. Нашим выражением if будет следующее.

if (y1>0-ball_mc._height/2 && y1<vy1){
. . .
}

Сейчас мы немного оптимизируем данный код. Если вы последовательно читали эту лекции, вы заметили, что сначала мы выполняем hitTest, затем вычисляем набор значений, и после этого выполняем выражение if. Однако это выражение if использует только значения y1 и vy1. Несмотря на то, что нам, в конечном счете, могут понадобиться значения x1 и vx1, не имеет смысла вычислять их до того момента, как мы определим, нужны они или нет. Поэтому мы можем переместить эти строки с вычислениями внутрь блока if. Проверьте работу функции еще раз. Вы увидите, что скорость заметно возросла. Приведем окончательный код функции.

function checkWall(wall_mc) {
    // first do simple hitTest to see if it's close
    if (wall_mc.hitTest(ball_mc)) {
      // if so, determine ball's x and у position in relation to the wall
      x = ball_mc._x-wall_mc._x;
      у = ball_mc._y-wall_mc._y;
      // convert wall's angle to radians and compute cos and sin of it
      rad = wall_mc._rotation*Math. PI/180;
      cosAngle = Math.cos(rad);
      sinAngle = Math.sin(rad);
      // rotate у coord and velocity to align with wall angle
      y1 = cosAngle*y-sinAngle*x;
      vy1 = cosAngle*ball_mc.velY+sinAngle*ball_mc.velX;
      // check if ball is hitting wall
      if (y1>0-ball_mc._height/2 && y1<vy1) {
        // rotate x coord and velocity to align with wall angle
        x1 = cosAngle*x+sinAngle*y;
        vx1 = cosAngle*ball_mc.velX+sinAngle*ball_mc.velY;
        // do simple bounce calculation, adjusting position of ball
        // to align with edge of wall
        y1 = 0-ball_mc._height/2;
        vy1 *= bounce;
        // rotate coordinates back to original angle
        x = cosAngle*x1-sinAngle*y1;
        у = cosAngle*y1+sinAngle*x1;
        // rotate velocities back to original angle
        ball_mc.velX = cosAngle*vx1-sinAngle*vy1;
        ball_mc.velY = cosAngle*vy1+sinAngle*vx1;
        // adjust wall-relative position to stage position
        ball_mc._x = x+wall_mc._x;
        ball_mc._y = y+wall_mc._y;
      }
    }
}

Пример 8.7.

Наслаждайтесь результатом работы! Перед тем, как покинуть вас, я хочу продемонстрировать вам всю мощь того, что мы только что сделали. Сделайте четыре дополнительных копии фильма wall на рабочем столе. Назовите пять стен именами wall0_mc - wall4_mc. Расположите их в различных местах и поверните на разное число градусов. Теперь перейдите к функции move и замените строку

checkWall(wall_mc);

следующим кодом.

for (i=0; i<5; i++) {
checkWall (__root ["wal""+i+"_mc"] );
}

Это выражение обрабатывает циклом все стены, проверяя одну за другой на коллизии, и реализуя их поддержку в случае обнаружения столкновения.

Теперь все в ваших руках. Пользуясь приобретенными здесь навыками, вы можете создавать разнообразные Pinball-игры или игры типа "Donkey Kong".

Подведем итоги

В этой лекции мы рассмотрели очень много материала. Сделаем краткий обзор пройденного.

Теперь вы разбираетесь в основах тригонометрии.

Sin
Cos
Tan
Нахождение любой стороны или угла прямоугольного треугольника, имея минимум информации.
Движение фильма по окружности.
Нахождение расстояния между любыми двумя точками или фильмами.
Понятие радианов и градусов, а также преобразование их друг в друга.
Поворот фильма к определенной точке в определенной точке.

В области физики мы рассмотрели основы движения, включая скорость и ускорение, а также то, как раскладывать определенную скорость и ее угловое направление на скорости по направлению X и Y. Мы также рассмотрели пружинящие объекты, в которых я вижу практически неограниченный потенциал для создания интереснейших эффектов. Я постоянно продолжаю искать новые способы применения такого типа движения.

Комбинируя некоторые физические и тригонометрические принципы, мы реализовали объект, отскакивающий от нескольких расположенных под разными углами поверхностей - один из самых занимательных моментов в физике Flash.

При построении игры с астероидами мы применили практически все знания, полученные к тому моменту, и сделали эту игру очень похожей на оригинал. Это показатель того, насколько обширными являются ваши знания на данный момент. Сейчас вы знаете достаточно много для того, чтобы создавать некоторые стоящие игры и приложения. Применяйте эти знания совместно с вашим воображением и с остальным материалом, который вы изучите в следующих лекциях (рисование API, звук, видео и т.д.), и вас уже ничто не сможет остановить на пути успешного программирования во Flash!