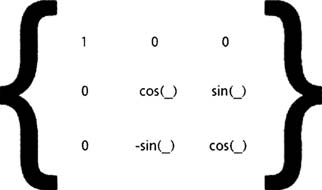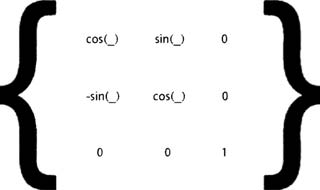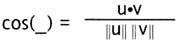Внимание! Для работы с этой лекцией необходимы учебные файлы, которые Вы можете загрузить  здесь.

Методы использования 3D

Перед тем, как приступать к рисованию API для создания 3D фигур в коде, ознакомимся с различными методами применения трехмерного содержимого в работе с Flash.

Предварительная прорисовка

Это наиболее простой способ, если у вас есть источники. Программы типа Electric Rain's Swift 3D посвящены созданию векторной графики для фильмов Flash. Electric Rain также производит надстройки для экспорта фильмов Flash из Discreet 3ds max, NewTek LightWave и Softimage. Electric Image Amorphium Pro также производит элементы Flash, которые могут быть применены напрямую в ваших фильмах. С помощью этих и других программ можно быстро прорисовывать изображения или наборы кадров анимации, и затем использовать ActionScript для управления изображениями внутри Flash. Недостатком этих программ является, конечно, их цена, а также размер файла экспортированного фильма, который в отдельных случаях может быть очень большим. Однако все эти программы позволяют получать изображения, которые выходят за рамки ограничений Flash, и чуть позже мы еще будем об этом говорить.

Приближенные иллюстрации

Поверьте мне, художники занимались трехмерной графикой задолго до появления микропроцессоров. Если вы хотите получить статическое трехмерное изображение, вам не имеет смысла гоняться за дорогим программным обеспечением для работы с трехмерной графикой. С помощью программы редактирования графики, такой как Adobe Photoshop, вы можете создавать псевдо-трехмерные изображения, которые выглядят вполне реалистично (посетите сайт Bert Monroy по адресу www.bertmonroy.com, чтобы ознакомиться с некоторыми потрясающими примерами). Даже работая во Flash, вы можете создавать интереснейшие 3D эффекты и рисунки, используя лишь средства для рисования и знания о перспективе и свойствах света.

3D в реальном времени

Прежде всего - зачем вам нужно читать эту лекцию. Немного математики - и вы сможете создать трехмерные объекты в реальном времени, используя исключительно код программы. Здесь вам очень поможет рисование API, так как создавать полигоны и применять заливку к ним в режиме реального времени теперь возможно. Несмотря на то, что вы могли делать это во Flash 5 искривлением треугольников, это было далеко не идеальным решением, так как в объектах часто появлялись провалы, а вычисления искривления сильно загружали процессор.

Загрузка процессора все еще актуальна при работе с 3D в Macromedia Flash MX, однако здесь уже есть способы упрощения для определенного содержимого. Например, не стоит пытаться создавать законченные анимированные трехмерные объекты с помощью одного лишь ActionScript. Вы же не собираетесь создавать голограмму! Если вы хотите изучать полностью интерактивные трехмерные миры, обратитесь к старшему брату Flash - Macromedia Director. Несмотря на дебаты в интерактивных форумах Flash на тему преимуществ Director над нашей любимой программой, Director просто более мощная программа. Возможности трехмерной графики ее последней версии просто фантастические и не могут быть реализованы во Flash.

Но подождите! Перед тем, как забрасывать эту книгу с мыслями о том, что вы приобрели ненужную программу, вспомните, что преимущества Flash 3D более весомы, чем Shockwave 3D (результат работы Director). Например, Flash Player гораздо более распространен, нежели Shockwave Player. Это означает, что больше людей сможет немедленно просматривать и наслаждаться результатами вашей 3D работы во Flash, в то время как им, вероятно, пришлось бы загружать значительно больший по размеру проигрыватель для просмотра вашего содержимого Shockwave 3D. Также, из-за сложности некоторых сред Shockwave 3D, его файлы намного больше, и, нередко, слишком велики для пользователей с низкоскоростным каналом доступа. До тех пор, пока будут распространены широкополосные сети, Flash будет в выигрыше.

Обзор концепций трехмерной графики

Если вы хотите применять на практике трехмерную графику в режиме run-time, нужно хотя бы вкратце знать основные концепции 3D перед началом работы с кодом Flash 3D. В этой лекции я подразумеваю, что вы немного знакомы с некоторыми из этих концепций, тем более что литературы по этому вопросу издано немало. Таким образом, мы сможем быстро перейти к занимательному процессу использования рисования API для расширения этих стандартных концепций и методов.

Оси

Экран монитора имеет две оси - x и y. Вы постоянно используете их при работе с параметрами _x, _y, _xscale и _yscale объектов. В трехмерной графике, как видно из ее названия, есть третье измерение, представляемое осью z, которая направлена перпендикулярно поверхности экрана. На этой оси располагаются точки, определяющие глубину и создающие иллюзию трехмерности. В нашем коде положительным значением на оси z является то, которое расположено ближе к наблюдателю.

Вершины

Наименьшим объектом в трехмерном мире является вершина, которая представляет из себя точку в трехмерном пространстве, имеющую три координаты x, y и z. Вершины являются составными частями трехмерных объектов.

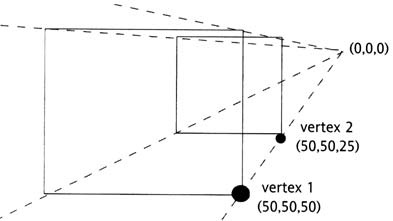
Глубина

Так как мы имеем дело с двухмерным выводом информации (экран монитора), нам необходим способ преобразования 3D координат в 2D пространство. Это делается настройкой параметров _x и _y наших вершин (не путать с трехмерными координатами вершины x и y) по значению z вершины. Чем больше значение z, тем ближе вершина находится к наблюдателю, и, следовательно, тем дальше вершина отодвинута от центра нашего пространства, играющего роль двумерной удаляющейся точки. Ниже приведена упрощенная схема этого процесса.

Несмотря на то, что у вершин 1 и 2 одинаковые 3D-значения x и y (вспомните, что трехмерные значения являются отдельными от координат экрана Flash), их z-значение изменяется, поэтому нам нужно моделировать глубину между двумя точками. Вершина 1, имеющая большее значение z, находится дальше от центра пространства. Так достигается моделирование глубины. Вот формула для выяснения того, каким образом перемещается вершина.

focalLength - это расстояние между наблюдателем и экраном. Для случая, описанного выше, мы установили focalLength на значение 100. Для вершины 2 переменная размера равна 1.33, при этом параметры _x и _y равны -66.5 и 133, соответственно. Это расстояние до вершины от центра в пикселях. Вершина 1 с переменной размера, имеющей значение 2, установит значения _x и _y на величины -100 и 200, соответственно. Координаты вершины (их координаты отличны от 3D-координат) заданы от центра пространства. Настраивая focalLength, мы можем увеличивать или уменьшать искажение перспективы.

Векторы

Мы будем говорить об этих объектах далее, при обсуждении света, однако сейчас надо иметь в виду, что вектор - это количественная величина в трехмерном пространстве, состоящая из направления и модуля. Представьте себе прожектор в театре, светящий вниз на артиста, находящегося на сцене. Это вектор, так как у света прожектора есть направление, а луч имеет определенную длину.

Матрицы

Матрицы, как вы помните - это прямоугольные массивы чисел. Мы будем использовать матрицы в преобразовании нашего трехмерного мира, во многом аналогично тому, как мы это делали в предыдущей лекции с градиентами.

Это основные идеи и термины, которые вам необходимо знать. Теперь перейдем к реализации этих идей во Flash.

Создание куба

В этом упражнении мы будем создавать файл Flash 3D для демонстрации концепций, рассмотренных до сих пор, а также для создания основы, от которой мы сможем отталкиваться в дальнейшем: это будет вращающийся куб.

Установка вершин

1. Создайте новый фильм и сохраните его в файле spinning_cube_0.fla. Создайте новый символ фильма с центральной точкой регистрации с именем vertex и нарисуйте небольшой круг (я нарисовал круг диаметром 12,5). В меню Linkage Properties отметьте опцию Export for ActionScript и введите имя идентификатора vertex.

   Теперь у нас есть символ vertex в Library. В конечном счете, вершины будут лишь объектами в памяти и больше не будут символами фильма, однако в этом упражнении мы используем их в качестве символов. Теперь перейдем к программе.

    
2. Вернитесь в главную точку временной шкалы и переименуйте слой по умолчанию, присвоив ему имя actions. В кадре 1 введите следующий код.
   this.createEmptyMovieClip("center", 0);
   center._x = Stage.width/2;
   center._y = Stage.height/2;
   focalLength = 400;
   

   Мы создали фильм, который будет содержать наш трехмерный мир, и расположили его по центру рабочего места. Также установим переменную focalLength (которую используем для имитации глубины) на значение 400.

    
3. Далее мы создаем модель куба, определяя вершины. Добавьте следующий код под предыдущим кодом программы.
   cube = {};
   cube .vertexList = [];
   cube.vertexList.push({x:-50, y:-50, z:50});
   cube.vertexList.push({x:50, y:-50, z:50});
   cube.vertexList.push({x:50, y:-50, z:-50});
   cube.vertexList.push({x:-50, y:-50, z:-50});
   cube.vertexList.push({x:-50, y:50, z:50});
   cube.vertexList.push({x:50, y:50, z:50});
   cube.vertexList.push({x:50, y:50, z:-50});
   cube.vertexList.push({x:-50 , y:50, z:-50});
   vertices = [];
   for (i=0; i<cube.vertexList.length; i++) {
     center.attachMovie("vertex", "v"+i, i);
     vertices.push(center["v"+i]);
   }
   

   cube - это новый объект, которому мы присвоили единственный параметр vertexList. Это будет массив для содержания каждой отдельной вершины. В следующих восьми строках мы вставляем вершины в массив. Заметьте, что каждая вершина является отдельным объектом, имеющим три параметра: x, y и z. С использованием длины нашего массива мы располагаем физические вершины (символ, хранимый в Library) на рабочем месте для представления вершин нашего куба. Мы вставляем ссылку на этот фильм в наш массив vertices. Это то, с чем мы будем иметь дело при использовании рисования API для создания трехмерных визуальных эффектов.

    
4. Теперь нам нужно написать код, который будет располагать вершины на корректных позициях на экране.
   render = function (model) {
     for (var i = 0; i<model.vertexList.length; i++) {
       var scale = focalLength/(focalLength-model.vertexList[i].z) ;
       vertices[i]._x = model.vertexList[i].x*scale;
       vertices[i]._y = model.vertexList[i].y*scale;
     }
   };
   render(cube);
   

   render выполняется для vertexList нашей модели и устанавливает позицию на экране каждой вершины с использованием формулы глубины, о которой говорилось ранее. После этого наша функция вызывается. Запустите фильм и посмотрите на результат.

    

    

   
   
   

    

    

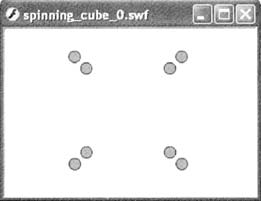
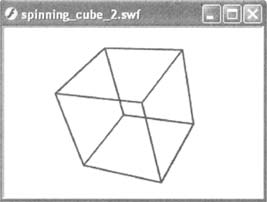
   spinning_cube_0.swf показывает искажение перспективы, примененное к восьми вершинам, определяющим куб. Моделирование глубины необходимо при отображении 3D-объекта на двухмерном устройстве вывода, которым является монитор компьютера.

    

   Имейте в виду, что мы не меняем размер или глубины наших вершин, как вы можете предположить. Это по той причине, что мы не пытаемся рисовать перспективные сферы, как это часто наблюдалось в экспериментах с Flash 5, а рисуем вершины, которые будут определять полигоны. Вершины сами по себе не меняют размер.

    

   Все до сих пор не слишком впечатляет: куб не вращается, поэтому сейчас трудно наблюдать расположение вершин. Сейчас мы это изменим.

    
5. Введите этот код сразу после функции render.
   rotateY = function (model, degree) {
     var sin = Math.sin(degree*Math.PI/180);
     var cos = Math.cos(degree*Math.PI/180);
     for (var i = 0; i<model.vertexList.length; i++) {
       var x = cos*model.vertexList[i].x-sin*model.vertexList[i].z;
       var z = cos*model.vertexList[i].z+sin*model.vertexList[i].x;
       model.vertexList[i].z = z;
       model.vertexList[i].x = x;
     }
   };
   

   Этот фрагмент кода будет поворачивать вершины нашей модели около оси y пространства. Сначала мы находим sin и cos нашего угла (в градусах, поэтому необходимо преобразовать число в радианы), а затем обрабатываем каждую вершину в нашей модели и перемещаем вершину по установленному углу. Формулы для поворота вокруг осей известны, и для экономии времени я продолжу рассказ, подразумевая, что вы согласны с их правильностью.

    
6. Наконец, замените последнюю строку render(cube); следующим кодом.
   center.onEnterFrame = function() {
     rotateY(cube, 3);
     render(cube);
   };
   

   Этот окончательный код поворачивает наш куб на три градуса около оси y и затем перерисовывает его на экране. Запустите ваш фильм, чтобы отобразить вращающийся куб. (Если здесь вы получите какие-либо неожиданные результаты, вы можете сравнить ваш файл с файлом spinning_cube_0.fla, находящимся на компакт-диске).

    

Добавление линий слияния

Первое, что необходимо сделать для более аккуратного моделирования трехмерного куба - это соединить вершины модели с помощью линий для создания каркаса. Это можно было сделать уже во Flash 5, но во Flash MX это намного проще, так как здесь можно использовать рисование API.

1. Сохраните имеющийся фильм в файле spinning_cube_1.fla. Теперь мы добавим код в нашу функцию прорисовки для рисования линий между вершинами. Для этого необходимо знать, какие вершины должны быть соединены друг с другом. Это сделать, добавив стороны к нашей модели, состоящие из выделенных вершин. Введите следующий код сразу после предыдущих строк, определяющих вершины cube (под последней строкой, начинающейся с cube.vertex.push).
   cube, side = [];
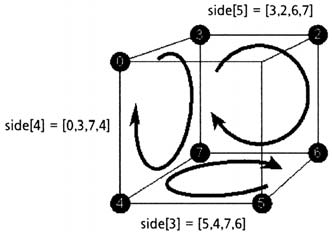
   cube.side.push([0, 1, 2, 3]);
   cube.side.push([2, 1, 5, 6]);
   cube.side.push([1, 0, 4, 5]);
   cube.side.push([5, 4, 7, 6]);
   cube.side.push([0, 3, 7, 4]);
   cube.side.push([3, 2, 6, 7]);
   

   side - это еще один параметр массива нашей модели. Каждый индекс состоит из четырех вершин, которые формируют сторону куба (попробуйте растянуть ее, чтобы увидеть, как это повлияет на связанные вершины). Порядок, в котором расположены вершины в каждом индексе side, очень важен, и вы убедитесь в этом, когда мы будем рассматривать процесс выбраковывания, заключающийся в том, что все стороны, не наблюдаемые пользователем, становятся невидимыми (это снижает загрузку процессора). Скоро мы это обсудим. А сейчас просто убедитесь в том, что вы сохранили порядок вершин для каждой стороны (порядок сторон неважен).

    
2. Теперь нужно отредактировать нашу функцию вручную для непосредственного рисования линий между вершинами. С определенными сторонами данный процесс является очень простым. Добавленный код выделен жирным шрифтом.
   render = function (model) {
     center.clear();
     center.lineStyle(2, 0, 100);
     for (var i=0; i<model.vertexList.length; i++) {
       var scale = focalLength/(focalLength-model.vertexList[i].z);
       vertices[i]._x = model.vertexList[i].x*scale;
       vertices[i]._y = model.vertexList[i].y*scale;
     }
     for (var i = 0; i<model. side, length; i++) {
       center.moveTo (vertices [model.side[i][0]] -_x,
       Кvertices [model.side[i][0] ]._y);
       for (var j = 1; j <model.side[i] .length; j++) {
         center.lineTo(vertices[model.side[i][j]]._x,
         Кvertices [model.side[i][j]]._y);
       }
       center.lineTo(vertices[model.side[i][0]]._x,
       Кvertices [model.side[i][0]]._y);
     }
   };
   

   После удаления и переопределения нашего lineStyle проходим циклом через все наши стороны и рисуем линии между всеми вершинами. Начинаем с движения карандаша к вершине в индексе 0 нашей текущей стороны. После этого рисуем линию, соединяющую все остальные вершины на стороне, заканчивая рисованием линии к исходной вершине. Сейчас запустите ваш фильм, чтобы увидеть линии получившегося каркаса.

    

    

   
   
   

    

    

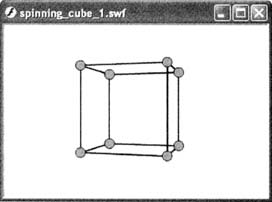
   Линии, нарисованные в API, добавлены для определения граней нашей модели.

    

   Теперь, когда есть линии каркаса, фильмы вершин стали несколько лишними. Мы можем удалить их все вместе и сделать так, чтобы вершины существовали отдельно в памяти компьютера. Нужно будет найти экранные координаты x и y вершин, не имея возможности посмотреть параметры _x и _y фильма.

    

    

    
3. Удалите символ вершины из Library, так как он больше не понадобится. Также удалите следующий код из вашего сценария (это строки 23-26 в панели Script).
   for (i=0; i<cube.vertexList.length; i++) {
     center.attachMovie("vertex", "v"+i, i);
     vertices.push(center["v"+i]);
   }
   
4. Теперь обновите вашу функцию render следующим образом.
   render = function (model) {
     center.clear ();
     center.lineStyle(2, 0, 100);
     verts2D = [];
     for (var i = 0; i<model .vertexList.length; i++) {
       verts2D[i] = {};
       var scale = focalLength/(focalLength-model.vertexList[i].z);
       verts2D[i].x = model.vertexList[i].x*scale;
       verts2D[i].y = model.vertexList[i].y*scale;
     }
     for (var i = 0; i<model.side.length; i++) {
       center.moveTo(verts2D[model.side[i][0]] .x,
         verts2D [model.side [i][0]] .y);
       for (var j =1; j<model.side[i] .length; j++) {
         center.lineTo(verts2D[model.side[i][j]] .x,
           verts2D [model. side [i][j]] .y);
       }
         center. lineTo(verts2D [model .side [i][0]] .x,
         Кverts2D [model. side [i][0]] .y);
       }
   };
   

   Этот вариант не сильно отличается от предыдущего. Мы создали новый массив с именем verts2D, который будет содержать объекты, состоящие из наших установленных экранных координат. При обработке циклом наших сторон и вершин, мы ищем в массиве verts2D эти значения. Имея лишь несколько дополнительных линий (на самом деле, мы удалили больше, чем добавили), мы создали трехмерный вращающийся куб только с использованием ActionScript.

    

    

   
   
   

    

    
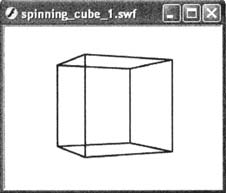
5. После удаления вершин фильма трехмерная модель вращается около оси y, и это результат работы только лишь рисования API.
6. Сохраните ваш фильм и оставьте его открытым, так как мы будем изменять его еще раз, когда разберем еще немного теории.

Матрицы преобразования

Теперь мы поговорим еще об одном способе реализации преобразования. При любом вращении около оси y (вы сами можете составить код для вращения вокруг двух других осей) мы обрабатываем циклом каждую вершину и соответствующим образом настраиваем координаты. Было бы неплохо осуществлять это только один раз, после вычисления всех необходимых преобразований. Это можно реализовать с помощью матриц.

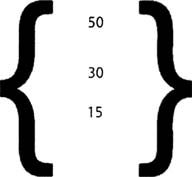
Каждая вершина также может быть описана матрицей без надобности настройки какого-либо кода. Вершина с координатами (50,30,15) может быть записана в следующем виде:

Вам не нужно ничего менять в коде (в панели ActionScript нельзя применять подобный формат), поскольку вы понимаете, что значит эта матрица. Что же она собой представляет? Вы видели, с какой легкостью мы смогли реализовать преобразования в наших градиентах с использованием преобразований, хранимых в матрицах? Так вот, мы можем сделать то же самое применительно к 3D-преобразованиям.

В нашем последнем упражнении, например в функции rotateY, преобразование обеспечивалось следующим образом.

Закомментированная строка отсутствовала в предыдущем коде. Я ее вставил, чтобы вы имели ее в виду.

Эта формула преобразования может быть сохранена в матрице преобразования, которую можно умножить на наши 3D-координаты. Эти матрицы преобразования могут быть непосредственно перемножены друг на друга, после чего получится кумулятивная матрица преобразования, и нам нужно просто провести умножение на наши координаты один раз в конце преобразований. Это помогло бы сохранить процессорное время и помочь в наших будущих преобразованиях. Итак, матрица преобразования для кода, указанного выше, выглядит так.

Результат умножения данной матрицы 3х3 на координатную матрицу 3х1 даст нам другую матрицу.

Это вам знакомо, не правда ли? Да, это та же формула, которая использовалась функцией rotateY, рассмотренной выше! Сейчас вам кажется, что использовать эту матрицу гораздо сложнее, нежели ее предшественницу, однако если настроить формулу один раз (что сводится к операциям умножения и сложения), вы сможете использовать ее во всех остальных преобразованиях. Вот они.

1. Преобразование около оси x

    

   
   
   

    

    
2. Преобразование около оси z

    

   
   
   

    

    
3. Изменение размера объекта

    

   
   
   

    

    

Давайте применим некоторые моменты в нашем коде, чтобы можно было легко осуществлять наши преобразования.

Преобразования с помощью матриц

1. Сохраните фильм из прошлого упражнения в файле spinning_cube_2.fla. Затем введите следующий код после функции render.
   rotateX = function (model, degree) {
     var rad = degree*Math.PI/180;
     var sin = Math.sin(rad);
     var cos = Math.cos(rad);
     var matrix = {a:l, b:0, c:0, d:0, e:cos, f:sin, g:0, h:-sin, i:cos};
     transform(matrix, model);
   };
   rotateY = function (model, degree) {
     var rad = degree*Math.PI/180;
     var sin = Math.sin(rad);
     var cos = Math.cos(rad);
     var matrix = {a:cos, b:0, c:-sin, d:0, e:l, f:0, g:sin, h:0, i:cos};
     transform(matrix, model);
   };
   rotateZ = function (model, degree) {
     var rad = degree*Math.PI/180;
     var sin = Math.sin(rad);
     var cos = Math.cos(rad);
     var matrix = {a:cos, b:sin, c:0, d:-sin, e:cos, f:0, g:0, h:0, i:l};
     transform(matrix, model);
   };
   scale = function (model, percent) {
     var rad = degree*Math.PI/180;
     var matrix = (a:percent, b:0, c:0, d:0,
       e:percent, f:0, g:0, h:0, i:percent};
     transform(matrix, model);
   };
   

   Эти матрицы легко представить в виде линейных массивов, однако я выбрал способ, аналогичный тому, что мы делали при преобразовании градиентов в предыдущей лекции, чтобы подчеркнуть разницу. После создания матрицы мы вызываем функцию transform для добавления этой матрицы в полное преобразование. Создадим эту функцию в следующем шаге.

    
2. Под определениями матриц, добавленными в предыдущем шаге, введите следующий код.
   transform = function (matrix, model) {
     if (transformMatrix) {
       var a = matrix.a*transformMatrix.a+matrix.b*transf onrmMatrix.d
       К+matrix.c* transformMatrix.g ;
       var b = matrix.a*transfo:irmMatrix.b+matrix.b*transf ormMatrix.e
       К+matrix.c*transformMatrix.h;
       var c = matrix.a*transformMatrix.c+matrix.b*transformMatrix.f
       К+matrix.c*transformMatrix.i;
       var d = matrix.d*transformMatrix.a+matrix.e*transformMatrix.d
       К+matrix.f*transformMatrix.g;
       var e = matrix.d*transformMatrix.b+matrix.e*transformMatrix.e
       К+matrix.f*transformMatrix.h;
       var f = matrix.d*transformMatrix.c+matrix.e*transformMatrix.f
       К+matrix.f*transformMatrix.i;
       var g = matrix.g*transformMatrix.a+matrix.h*transformMatrix.d
       К+matrix.i*transformMatrix.g;
       var h = matrix.g*transformMatrix.b+matrix.h* transformMatrix.e
       К+matrix.i*transformMatrix.h;
       var i = matrix.g*transformMatrix.c+matrix.h*transformMatrix.f
       К+matrix.i*transformMatrix.i;
       transformMatrix = {a:a, b:b, c:c, d:d, e:e, f:f, g:g, h:h,i:i};
     } else {
       transformMatrix = matrix;
     }
   };
   

   Хотя этот код кажется громоздким, он является лишь формулой умножения матрицы 3х3 на другую матрицу 3х3. В этой функции сначала проверяем, существует ли уже матрица преобразования. Если это так, мы умножаем две матрицы друг на друга, что формирует кумулятивную матрицу, состоящую из двух (если матрица преобразования еще не существует, мы создаем такую матрицу и приравниваем ее к матрице, отправленной нашей функции). В результате мы можем комбинировать несколько преобразований в одной матрице перед тем, как применять его к нашим вершинам. Посмотрим, как это делается.

    
3. Введите следующий код в функцию render.
   render = function (model) {
     if (transfonriMatrix) {
     for (var i = 0; i<model.vertexList.length; i++) {
       var vert = model.vertexList[i];
       var x = transformMatrix.a*vert.x+transformMatrix.b*vert.y
       К+transformMatrix.c*vert.z;
       var y = transformMatrix.d*vert.x+transformMatrix.e*vert.y
       К+transformMatrix.f*vert.z;
       var z = transformMatrix.g*vert.x+transformMatrix.h*vert.y
       К+transformMatrix.i*vert.z;
       vert.x = x;
       vert.y = y;
       vert.z = z;
     }
     delete transformMatrix;
   }
     center.clear();
     center.lineStyle(2, 0, 100);
     verts2D = [];
     for (var i = 0; i<model .vertexList. length; i++) {
       verts2D[i] = {};
       var scale = focalLength/(focalLength-model.vertexList[i].z);
       verts2D[i].x = model.vertexList[i].x*scale;
       verts2D[i].y = model.vertexList[i].y*scale;
     }
     for (var i = 0; i<model.side.length; i++) {
       center.moveTo(verts2D[model.side[i][0]].x, verts2D [model.side [i][0]] .y);
       for (var j = 1; j<model.side[i].length; j++) {
         center.lineTo(verts2D[model.side[i][j]].x, verts2D [model, side [i][j]].y);
     }
     center.lineTo(verts2D[model.side[i][0]].x,
     verts2D[model.side[i][0]].y);
     }
   };
   

   Пример 10.1.

   Наконец, перед прорисовкой модели на экране нужно применить наши преобразования (которые удобным образом сохранены в одной матрице) к вершинам. Дополнительным кодом является основная формула умножения матрицы 3х3 (нашего преобразования) на матрицу 3х1 (координаты каждой вершины). После этого мы удаляем наше преобразование для подготовки к дальнейшим преобразованиям.

    
4. Для вызова наших новых функций преобразования измените функцию onEnterFrame в конце кода следующим образом.
   center.onEnterFrame = function() {
     rotateX(cube, 3);
     rotateY(cube, 6);
     rotateZ(cube, 10);
     render(cube);
   };
   

   Несмотря на то, что мы осуществляем три отдельных преобразования, они не будут применены к модели, пока не будет вызвана функция render, один раз в каждом кадре. Запустите фильм, чтобы увидеть результат работы.

    

    

   
   
   

    

    

   С помощью матриц преобразования размером 3х3, вращение нашей каркасной модели вокруг всех трех осей осуществляется более эффективно.

    

   Если вы получите какие-либо неожиданные результаты, сверьте ваш код с написанной мной программой в файле spinning_cube_2.fla на компакт-диске.

    

   Теперь мы уже кое-что умеем! Даже несмотря на то, что мы имеем лишь вращающийся каркас куба, мы создаем что-то, что будет представлять собой хорошую базу для усовершенствования получаемых результатов.

    

Сортировка глубины

Одним из усовершенствований, которое нам будет необходимо сделать, когда мы дойдем до заливки моделей цветом, является сортировка глубины, или метод z-сортировки. Это метод размещения моделей или сторон куба, которые находятся ближе к наблюдателю, перед объектами и сторонами, которые находятся дальше. Как правило, не нужно, чтобы объект со значением координаты z=-200 был впереди объекта с координатой z=50. Во Flash 5 для этого нужно было бы поменять глубины фильмов вершин. Теперь, во Flash MX, мы можем просто создать порядок рисования, начиная с самых дальних сторон и далее по направлению к наблюдателю, прорисовывая стороны, которые будут располагаться за ними. Это все будет реализовываться в функции render, как показано в следующем упражнении.

Закрашивание сторон

1. Сохраните фильм в файле spinning_cube_3.fla. Обновите функцию render, добавив в нее следующий код.
   render = function (model) {
     if (transformMatrix) {
       for (var i = 0; i<model.vertexList.length; i++) {
         var vert = model.vertexList[i];
         var x = transformMatrix.a*vert.x+transformMatrix.b*vert.y
         К+transformMatrix.c*vert.z;
         var y = transformMatrix.d*vert.x+transformMatrix.e*vert.y
         К+transformMatrix.f*vert.z;
         var z = transformMatrix.g*vert.x+transformMatrix.h*vert.y
         К+transformMatrix.i*vert.z;
         vert.x = x;
         vert.y = y;
         vert.z = z;
       }
       delete transformMatrix;
     }
     center.clear ();
     center.lineStyle(2, 0, 100);
     verts2D = [];
     depthArray = [];
     for (var i = 0; i<model.side.length; i++) {
       var zDepth = 0;
       for (var j = 0; j<model.side[i].length; j++) {
         var whichVert = model.side[i] [j];
         if (verts2D[whichVert] == undefined) {
           verts2D[whichVert] = {};
           var scale = focalLength/(focalLength
           К-model.vertexList[whichVert].z);
           verts2D[whichVert].x = model.vertexList[whichVert].x*scale;
           verts2D[whichVert].y = model.vertexList[whichVert].y*scale;
         }
         zDepth += model.vertexList[whichVert].z;
       }
       depthArray.push([model.side[i], zDepth]);
     }
     depthArray.sort(function (a, b) { return a[1]>b[1];});
     for (var 1 = 0; i<depthArray.length; i++) {
       var sideVerts = depthArray[i][0];
       center.moveTo(verts2D[sideVerts[0]].x,verts2D [sideVerts [0]].y);
       center.beginFill0x666666, 100);
       for (var j =1; j<sideVerts.length; j++) {
         center.lineTo(verts2D[sideVerts[j]].x,verts2D [sideVerts [j]].y);
       }
       center.lineTo(verts2D[sideVerts[0]].x,verts2D[sideVerts [0]].y);
       center.endFill();
     }
   };
   

   Пример 10.2.

   Довольно много изменений, однако они значительно влияют на работу функции. Мы имеем несколько вложенных массивов, в которых можно запутаться, поэтому давайте разберем этот код и посмотрим, какие действия он выполняет.

    

   Сначала мы создаем массив с именем depthArray. Он содержит ссылки на стороны нашей модели и общую позицию z каждой вершины в данной стороне (это даст вполне подходящий уровень z для наших целей). После этого мы обрабатываем циклом каждую сторону нашей модели и преобразовываем ее вершины в двухмерные координаты (которые ничем не отличаются от оных в нашей предыдущей версии), а также добавляем значение z каждой вершины к этой величине zDepth. Выражение if используется таким образом, что не выполняется никаких необязательных операций по замене более чем один раз для вершины, что могло бы иметь место, так как стороны имеют общие вершины с другими сторонами.

    

   Как только вершины преобразованы и величина zDepth каждой стороны записана, мы вставляем ссылку на каждую сторону (которая, как вы знаете, содержит вершины этой стороны) и ее значение zDepth в массив depthArray, который сразу сортируется с помощью функции сортировки. Мы использовали практически идентичную функцию сортировки в предыдущей лекции, но здесь мы можем включать ее непосредственно в аргументы сортировки вместо вызова ее извне. Как только depthArray становится упорядоченным (в направлении от самой дальней стороны к самой ближней), мы обрабатываем его циклом и затем рисуем наши линии и заливки.

    

   В коде выше вас могут вводить в заблуждение две переменныe: whichVert и sideVerts, поэтому давайте рассмотрим их более детально. whichVert содержит просто номер вершины для стороны в модели. Поэтому для side[0], которая является массивом чисел [0,1,2,3], whichVert будет принимать значение каждого индекса на соответствующей итерации цикла. sideVerts, с другой стороны, будет содержать весь массив номеров вершин. Помните, что каждый индекс depthArray содержит ссылку на одну из сторон модели и ее zDepth. Выяснив первую позицию индекса в определенном индексе depthArray, мы можем получить список вершин этой стороны, чтобы затем поместить их в sideVerts.

    
2. Запустите ваш фильм. Теперь стороны куба закрашены, и все благодаря рисованию API!

    

   
   
   

    

    

   spinning_cube_3.swf демонстрирует модель куба с закрашенными гранями и видимыми ребрами, полностью созданную с помощью рисования API. Сортировка глубины каждого полигона позволяет ближним сторонам отображаться перед более дальними сторонами. Куб вращается вокруг всех трех осей в каждом кадре с помощью матриц преобразования 3х3.

    
3. Сохраните фильм и оставьте его открытым для следующего упражнения.

Выбраковка задних поверхностей

Выбраковка задних поверхностей - это предотвращение прорисовки полигонов, не видимых наблюдателю, что сохраняет процессорное время (на самом деле нормаль полигона направлена от пользователя, но, к сожалению, здесь нет возможности вдаваться в такие подробности). Способ определения того, виден полигон наблюдателю или нет, заключается в проверке экранных координат его вершин (но не трехмерных координат!), так как это положение модели относительно экрана и наблюдателя, что является важным определяющим фактором видимости полигонов. Нам также необходимо знать порядок расположения вершин - по часовой или против часовой стрелки. В нашем методе необходимо, чтобы вершины были определены для стороны в направлении против часовой стрелки относительно центра объекта, чтобы они были видны под корректными углами.

Все это звучит немного запутанно, не так ли? Как только вы поймете смысл происходящего, вы сразу поймете, что сложного здесь ничего нет. Поверьте мне. На самом деле, проверка является наиболее замысловатой частью. Процесс, используемый мной для определения порядка вершин, заключается в мысленном представлении полигона (или стороны), которая "смотрит" прямо на меня с левой от центра стороны по ходу движения. В случае с нашей моделью, это было бы мысленное вращение куба с отображением каждой стороны так, чтобы я мог лучше наблюдать порядок вершин. Если после этого поместить вершины в массив side в порядке против часовой стрелки в текущем отображении модели, сторона будет полностью видна наблюдателю, когда будет находиться с левой стороны от центра. Для лучшей визуализации этого процесса мы рассмотрим модель куба с тремя из сторон, определенными таким образом, что противоположная сторона куба также видна наблюдателю.

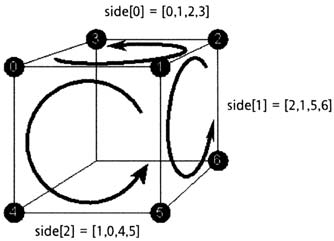
Здесь может показаться, что просто нужно определить все стороны в порядке против часовой стрелки относительно наблюдателя. Однако давайте рассмотрим порядок для трех остальных сторон.

Ага! По часовой стрелке! Это потому, что в данном положении куба нам не нужно прорисовывать эти стороны, так как они находятся внутри куба. Именно по этой причине я использую процедуру, описанную выше, и заключающуюся в мысленном повороте модели так, чтобы мне стала видна каждая сторона объекта перед записью порядка вершин. Если повернуть side[5] так, чтобы она "смотрела" на меня слева от центра, тогда порядок ее вершин будет определяться в направлении против часовой стрелки.

Итак, вершины, расположенные на экране по часовой стрелке, не должны прорисовываться. Теперь нужно определить порядок, в котором отображаются двухмерные координаты вершин в данный момент. (Для получения более полной информации можете обратиться к сайту Pavils Jurjans www.jurjans.lv/flash, чтобы ознакомиться с открытым исходным кодом и материалом по этой интересной теме.)

Прорисовка только необходимых объектов

1. Сохраните фильм из предыдущего упражнения в файле spinning_cube_4.fla. Создайте новую функцию над функцией render (на самом деле, не имеет значения, в каком месте кода вы ее расположите, однако, расположив ее в указанном месте, вы сохраните логический порядок и структуру вашего кода).
   backface - function (x, y) {
     var cax = x[2]-x[0];
     var cay = y[2]-y[0];
     var bcx = x[l]-x[2];
     var bey = y[l]-y[2];
     return (cax*bcy<cay*bcx);
   };
   

   Здесь мы будем отправлять этой функции три вершины стороны. Используя экранные координаты трех вершин в формуле выше, можно определить, в каком порядке расположены вершины на экране - по часовой или против часовой стрелки. Нам нужны значения "истина" и "ложь". Значение "истина" имеет место, когда сторона "отвернута" от пользователя, а значение "ложь" (т.е. не "задняя" сторона) - если сторона повернута в направлении пользователя.

    
2. Для вызова этой функции мы просто добавим эти несколько новых строк в функцию render.
   depthArray.sort(function (a, b) { return a [1] >b [1] ;});
     for (var i = 0; i<depthArray.length; i++) {
       var sideVerts = depthArray[i][0];
         if (!backface([verts2D[sideVerts[0]].x,
         verts2D[sideVerts[1]] .x,
         Кverts2D [sideVerts [2]] .x], [verts2D [sideVerts [0]] .y,
         Кverts2D [sideVerts [1]] .y, verts2D [sideVerts [2]] .y])) {
         center.moveTo(verts2D[sideVerts[0]].x,
           verts2D [sideVerts [0]] .y);
         center.beginFill0x666666, 100);
         for (var j = 1; j<sideVerts.length; j++) {
           center.lineTo(verts2D[sideVerts[j]] .x,
             verts2D [sideVerts [j]] .y);
         }
         center.lineTo(verts2D[sideVerts[0]] .x,
           verts2D [sideVerts [0]] .y);
         center.endFill();
       }
     }
   };
   

   Здесь мы добавляем рисование линий и методы рисования в условное выражение, которое проверяет, повернута ли сторона лицевой поверхностью в направлении от пользователя. Если здесь не обрабатывать каждую вершину в вызове функции, пришлось бы это сделать в функции backface. Я думаю, что так понятнее. Мы помещаем координаты x и y первых трех вершин в отдельные массивы при вызове функции backface (посмотрите еще раз на эту функцию, чтобы увидеть, как осуществляется доступ к этим массивам после их отправки). Если функция backface определяет, что данная сторона не является противоположной (возвращается значение "ложь"), то эта сторона прорисовывается.

    
3. Запустите фильм. Применения сортировки по оси z не заметно.

    

   
   
   

    

    

   К нашему вращающемуся кубу применен процесс отмены прорисовки противоположных сторон. С его помощью стороны, находящиеся вне поля зрения наблюдателя, не прорисовываются за ненадобностью.

    
4. Однако, если вернуться к коду и заменить данные интенсивности заливки на 0 посредством замены вызова beginFill() на center.beginFill(0x666666, 0);, вы увидите, что отмена прорисовки действительно применена к противоположным сторонам куба.

    

   
   
   

    

    
5. Сохраните ваш фильм и оставьте его открытым. Мы будем обновлять его в следующем упражнении.

Подсветка полигонов

Мы получили довольно интересный эффект вращения сплошного куба на рабочем месте, однако не рассмотрели один важный фактор, необходимый для обеспечения реальности трехмерного изображения: динамическую подсветку модели. Для создания более реалистичной среды необходимо установить источник света, который будет освещать модель и создавать тени согласно углу от источника света.

Здесь появится более сложная математика, поэтому с нее я и начну этот параграф. Перед знакомством с Flash вся моя математика после высшего учебного заведения сводилась к подсчету счетов и сумм в ресторане. Формулы, которые будут использоваться здесь, являются результатом многих ночей, проведенных за компьютером на математических сайтах, а также помощи ahab - модератора форумов на сайте www.were-here.com. Мне также помогли друзья с более глубокими знаниями математики. Я хочу попросить вас использовать все доступные источники, которые могут оказать вам помощь. Не забывайте о книгах - в них есть все нужные формулы. Невероятные эффекты Flash будут достигнуты посредством комбинирования этих ресурсов с вашей изобретательностью, а не только с помощью математических выкладок.

Подсветка куба

Сначала необходимо создать источник света. Это можно сделать с помощью переменных, однако мы применим здесь объектно-ориентированный метод и сделаем источник света отдельным объектом (мы применим эту же концепцию в следующей лекции).

1. Сохраните фильм в файле spinning_cube_5.fla. Сразу в начале кода, перед всей имеющейся программой, введите следующее.
   LightSource = function(x, y, z, brightness) {
     this.x = x;
     this.y = y;
     this.z = z;
     this.brightness = brightness;
     this.calcMag = function() {
       this.magnitude = Math.sqrt
        (this.x*this.x+this.y*this.y+this.z*this.z);
     };
     this.calcMag();
   };
   

   Функция-конструктор LightSource создает новый источник света для нашего мира. Единственными ее параметрами являются позиция и яркость, которые устанавливаются при создании объекта (в конечном счете вам понадобится настраивать эти параметры с помощью методов). Метод calcMag вычисляет магнитуду источника света (расстояние от центра пространства до источника). Это значение понадобится нам позже, и нам также понадобится пересчитывать его при изменении параметров x, y или z.

    
2. Чтобы создать инстанс LightSource, введите следующий код после строки focalLength = 400; (она находится сразу после секции, к которой мы создаем фильм center, рядом с началом кода).
   light = new LightSource (-20000, -20000, 20000, 100);
   

   Итак, light теперь является LightSource, который используется в сцене, и если нам понадобится получить доступ к любому из его параметров, мы будем использовать выражение light.параметр. Мы установили его позицию на -20,000 по осям x и y, и на позицию 20,000 по оси z. При таком положении источника объект будет традиционно освещен спереди, сверху и слева. Мы также установили его яркость на значение 100. Потенциальные улучшения нашего исходного объекта LightSource могут включать в себя дополнительные методы для изменения яркости или для присвоения цвета нашему источнику.

    

   Теперь нам нужна переменная модели, которая будет содержать ее цвет. Мы могли бы просто установить цвет для всей модели целиком, однако интереснее присвоить цвет отдельно сторонам или полигонам. Давайте улучшим свойства стороны модели, после чего они будут содержать объекты с информацией о стороне, в противовес обычным ссылкам на номера вершин.

    
3. Измените шесть строк кода, которые вставляют номера вершин в массив side для чтения.
   cube.side = [];
   cube.side.push({vertices:[0,1,2,3], sideColor:0x6600CC});
   cube.side.push({vertices:[2,1,5,6], sideColor:0x6600CC});
   cube.side.push({vertices:[1,0,4,5], sideColor:0x6600CC});
   cube.side.push({vertices:[5,4,7,6], sideColor:0x6600CC});
   cube.side.push({vertices:[0,3,7,4], sideColor:0x6600CC});
   cube.side.push({vertices:[3,2,6,7], sideColor:0x6600CC});
   

   Вместо обычного добавления чисел в этот параметр, мы вставляем объекты, содержащие сами параметры: vertices для содержания номеров вершин и sideColor для содержания шестнадцатеричного значения цвета стороны.

    

   Мы реализовали хранение значений цветов. Нам нужно будет изменить несколько строк кода нашей функции render для обеспечения работы новой структуры. Сейчас рассмотрим весь код, чтобы определить влияние источника света на цвет в двух других функциях.

    
4. Внесите следующие изменения во вторую часть функции render.
   center.clear();
   center.lineStyle(2, 0, 100);
   verts2D = [];
   depthArray = [];
     for (var i = 0; i<model. side, length; i++) {
       var zDepth = 0;
       for (var j = 0; j<model.side[i].vertices.length; j++) {
         var whichVert = model.side[i].vertices[j];
         if (verts2D [whichVert] == undefined) {
           verts2D[whichVert] = {};
           var scale = focalLength/(focalLength-model.vertexList[whichVert].z);
           verts2D[whichVert].x = model.vertexList [whichVert].x*scale;
           verts2D[whichVert].y = model.vertexList [whichVert].y*scale;
         }
         zDepth += model.vertexList[whichVert].z;
       }
       depthArray.push([model.side[i], zDepth]);
     }
     depthArray.sort(function (a, b) { return a [1]>b [1];});
     for (var i = 0; i<depthArray.length; i++) {
       var sideVerts = depthArray[i][0].vertices;
       if (!backface([verts2D[sideVerts[0]].x, 
       Кverts2D [sideVerts [1]].x,verts2D [sideVerts [2]].x],
       К[verts2D [sideVerts [0]].y,
       Кverts2D [sideVerts [1]].y,verts2D [sideVerts [2]].y] ) ) {
         center.moveTo(verts2D [sideVerts [0]].x,verts2D [sideVerts [0]].y);
         center.beginFill(getSideColor(model,depthArray[i][0]), 100);
         for (var j = 1; j<sideVerts.length; j++) {
           center.lineTo(verts2D[sideVerts[j]].x,verts2D [sideVerts [j]].y);
         }
         center.lineTo(verts2D[sideVerts[0]].x,verts2D [sideVerts [0]].y);
         center.endFill();
       }
     }
   };
   

   Пример 10.3.

   Это небольшое обновление открывает новые возможности. У нас есть доступ к параметру стороны vertices, где хранятся номера вершин. Вместо предоставления цвета заливки в методе beginFill мы будем вызывать функцию, которой будем отправлять ссылку на текущую сторону (она хранится в массиве depthArray[i] [0]) и ссылку на саму модель. Она будет возвращать цвет, необходимый параметр для beginFill. Теперь напишем эту функцию.

    
5. Добавьте следующую новую функцию прямо под функцией render.
   getSideColor = function (model, side) {
     var col = side.sideColor.toString(16);
     while (col.length < 6) {
       col = "0" + col
     }
     var verts = [model.vertexList[side.vertices[0]],
     Кmodel.vertexList[side.vertices[1]],
     Кmodel.vertexList[side.vertices[2]]];
     var lightFactor = factorLightAngle(verts);
     var r = parseInt(col.substr(0, 2), 16)*lightFactor;
     var g = parseInt(col.substr(2, 2), 16)*lightFactor;
     var b = parseInt(col.substr(4, 2), 16)*lightFactor;
     return r << 16 | g << 8 | b;
   };
   

   getSideColor почти идентична функции convertToRGB из предыдущей лекции (там о ней было рассказано более подробно). Большая часть функции разделяет цвет на его красную, зеленую и синюю составляющие, чтобы можно было изменять каждое значение по отдельности. Отличаются лишь те строки, которые вставляют три вершины нашей стороны во временный массив переменных и затем отправляют этот массив функции с именем factorLightAngle. Посредством прямой отправки вершин (помните, объекты хранятся в vertexList нашей модели), factorLightAngle будет легче взаимодействовать с номерами.

    

   Осталось разобраться лишь с одной функцией - factorLightAngle - но в ней-то и заложен весь смысл. В ней вас также поджидают сложные математические выражения, поэтому соберитесь - и вперед!

    
6. Добавьте эти строки сразу после последней функции.
   factorLightAngle = function (vertices) {
     var U = [(vertices[0].x-vertices[1].x), (vertices[0].y
     Кvertices [1].y), (vertices[0].z-vertices[1].z)];
     var V = [(vertices[1].x-vertices[2].x), (vertices[1].y-
     Кvertices[2].y), (vertices[1].z-vertices[2].z)];
     var p = [((U[1]*V[2])-(U[2]*V[1])),
       - ( (U[0]*V[2]) - (U[2]*V[0])),
     К((U[0]*V[1])-(U[1]*V[0]))];
     var magP = Math, sqrt ((p[0]*p[0]) +
        (p[1]*p[1]) + (p[2]*p[2]));
     var dP = ((p[0]*light.x) + (p[l]*light.y) +
         (p[2]*light.z));
     return ((Math.acos(dP/
       (magP*light.magnitude))/Math.PI)
     К*light.brightness/100);
   };
   

7. Сейчас мы разберем, что происходит в этом коде. Запустив фильм, вы увидите, как по мере вращения вашего куба на него падает свет и создаются тени на гранях.
    

   К модели вращающегося куба применена динамическая подсветка, что обеспечивает более реалистичное симулирование глубины.

    

   Давайте сделаем шаг назад и разберемся в последней части кода. U и V - это просто трехмерные векторы, полученные из вершин (вспомните, что вектор здесь представляет собой позицию и направление в пространстве). Вы, вероятно, проделывали аналогичные вещи не один раз для двухмерных векторов в фильмах Flash, при вычитании параметра _x одного фильма из параметра _x другого (единственное отличие здесь в том, что у нас есть еще одно измерение, для которого также необходимо выполнять расчет). Узнав U и V, мы находим их векторное произведение, которое в результате даст вектор, перпендикулярный двум векторам, используемым в операции. В трехмерном пространстве, этот вектор перпендикулярен к поверхности и называется нормалью полигона. Эта нормаль говорит нам об ориентации поверхности полигона.

    

    

   
   
   

    

    

   Определив этот вектор, мы можем найти его отношение к нашему источнику света и определить, какое количество света он должен получать. Для этого использовалась следующая формула.

    

    

   
   
   

    

    

   Заметка: U и V использовались здесь для обозначения двух векторов и не относятся к переменным U и V, использованным выше.

    

   Что это значит? Для нахождения косинуса угла между источником света и нормалью полигона мы умножаем два вектора друг на друга (скалярное произведение, являющееся величиной расстояния между двумя векторами) и затем делим полученное число на произведение длин двух векторов (их магнитуды, или расстояние от центра пространства).

    

   Некоторые очень умные и знаменитые математики работали очень долго над этой формулой, и кто я такой, чтобы обсуждать ее? Я могу использовать эту формулу для нахождения угла, под которым свет падает на полигон, и это все, что мне необходимо.

    

   Перед тем, как мы перейдем к коду, использующему эту формулу, необходимо понять природу источника света, который мы разместили в нашей трехмерной сцене. В 3D-программах источник света сродни направленному свету, всегда направленному на точку в центре пространства. Это избавляет нас от необходимости ориентировать наш свет на модели при его первом размещении или при его изменении в процессе анимации. Однако, по этой причине, если свет перемещается на центр пространства, он не может быть направлен ни на одну из моделей, поэтому они будут черными и неосвещенными (черными, так как у нас не установлен источник рассеянного света в сцене; вы сможете установить этот источник позже).

    

   Остались три последние строки функции. magP является магнитудой для нашей нормали, которая является расстоянием полигона от центра пространства (здесь работает теорема Пифагора). dP содержит результат операции скалярного произведения - умножения и сложения двух компонентов вектора. Наконец, мы определяем угол нахождением арккосинуса нашего скалярного произведения деленного на магнитуды двух векторов. Это даст нам значение в радианах между нулем и пи, поэтому мы делим на пи, чтобы получить процентное значение. Мы используем это для нахождения процента яркости нашего источника света (делим на 100 еще раз из-за способа, который используется для установки яркости света - я хотел использовать целые числа для представления этого значения, поэтому нужно разделить на 100 для возвращения процентной величины этой функцией).

    

   Можете вздохнуть с облегчением - мы закончили упражнение. Однако, если вы хотите вернуться к какой-либо части этого упражнения (или к одной из ранних версий вращающегося куба), все исходные файлы FLA с комментариями находятся на компакт-диске. Вы можете сравнить их с созданными вами файлами, если возникнут какие-либо вопросы.

    

   В файле spinning_cube_final.fla я добавил текстовые поля, поэтому вы можете изменять преобразования куба и параметры света в режиме run-time. Я также добавил функцию translate, чтобы ваши модели могли двигаться от центра. В идеале, вам нужно применять этот способ (я сделал это на свой страх и риск). Одним из альтернативных методов является использование матрицы размером 4х4 для наших преобразований и добавление четвертого измерения для каждой вершины. Мы изучим это в следующей лекции. Это одно из улучшений, которое я вам советую сделать, если вы решили продолжить работу с этим фильмом.