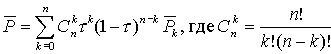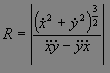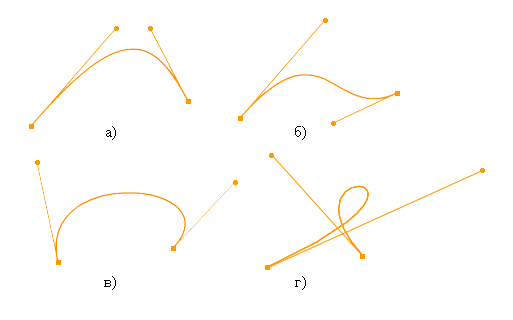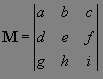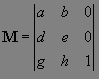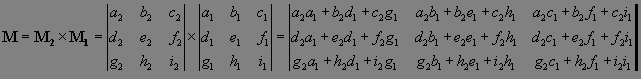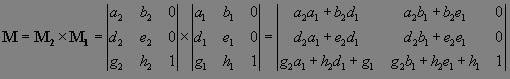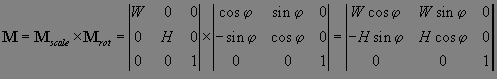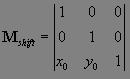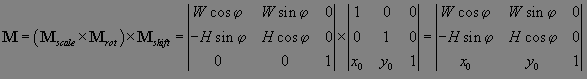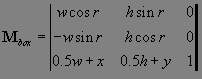|
Предыдущие версии Флэш (вплоть до Флэш 5) не имели
функций программного рисования. В чем-то такое решение
было оправдано: ведь Флэш предназначен для рисования в
design-time, то есть вручную - до запуска
анимации. И тем не менее возникали задачи (часто не
такие уж сложные), которые требовали именно программного
рисования. Это и эффекты, для которых потребовалось бы
слишком много ручной работы (например, градиент,
изменяющийся в каждом следующем кадре строго
определенным образом, или набор из огромного количества
определенным образом расположенных тонких линий). И, тем
более, - изображения, внешний вид которых сильно зависит
от действий пользователя и заранее совершенно неизвестен
(например, графики функций). Флэш МХ, наконец-то,
предоставляет нам все необходимые средства для решения
этих задач. И начнем мы изучение этих средств с самого
простого - прямых и кривых различного вида.
Рис. 10.1. Методы программного рисования во
Flash MX
Прямые и кривые
Итак, внутрь
любого клипа мы можем добавить программно нарисованные
прямые или кривые. Заметьте, что рисование происходит
именно в конкретном клипе (и будет сдвигаться вместе с
клипом или перекрываться вышележащими клипами). Приятное
свойство Флэша - это антиалиасинг проводимых линий.
Больше никаких "лесенок"!
Методы
программного рисования прямых во Флэше мало чем
отличаются от таковых в других языках программирования.
Поэтому начнем сразу с примера. Вот как выглядит код,
рисующий равносторонний треугольник.
//создаем MovieClip, в котором
хотим нарисовать треугольник
_root.createEmptyMovieClip("triang_mc", 1);
thickness = 1; //толщина линии
lineColor = 0xff0000; //цвет линии
alpha = 100; //прозрачность линии
//далее, передаем эти аргументы в метод,
определяющий стиль линии
triang_mc.lineStyle(thickness, lineColor, alpha);
//далее, определяем координаты вершин
Ax = 20; Ay = 100;
Bx = 120; By = 100;
Cx = 70; Cy = 100*(1-Math.sqrt(3)/2);
//и, наконец, собственно рисуем треугольник
triang_mc.moveTo(Ax, Ay); //ставим курсор в вершину
A
//соединяем вершины
triang_mc.lineTo(Bx, By);
triang_mc.lineTo(Cx, Cy);
triang_mc.lineTo(Ax, Ay);
Пример 10.1.
Обратите
внимание, что "холстом" для программно нарисованных
объектов является MovieClip
(в данном случае triang_mc).
Если в клипе есть объекты, вставленные в design-time,
то они будут отображаться поверх нарисованных через
ActionScript. Последние будут перемещаться и
поворачиваться, сжиматься и растягиваться, менять
прозрачность и цвет вместе с клипом, а также влиять на
_width и
_height.
На
_width и
_height хотелось бы
остановиться подробнее. В редакторе FlashMX с помощью
панелей Properties или Info мы можем
достаточно точно установить размеры объектов. И в праве
ожидать, что те же значения мы получим, спрашивая у
объекта значения _width и
_height в ActionScript. К
сожалению, это не всегда так. Например, создайте клип,
содержащий одну горизонтальную линию длиной 200 пикселей,
толщиной 10. В панели Properties или Info
вы увидите, что ширина этого клипа ровно 200.0 пикселей,
а высота - 0.0 (рис. 10.2 а). В размерах, которые вы
задаете в редакторе, толщина линий не учитывается. То же
самое можете проделать программно (рис. 10.2 б). А
теперь давайте посмотрим, как это выглядит в run-time
(рис. 10.2 в). Вы видите разницу между двумя черными
линиями, одна из которых нарисована в design-time,
другая - через ActionScript? Я тоже не вижу. А вот
flash-player видит. При измерении свойств
_width и
_height учитывается
конечная толщина линий. При этом для объектов,
вставленных в design-time и для нарисованных в
ActionScript, учитывается по-разному (см. окно Output
на рис.
10.2
б). Во втором случае к "номинальным" размерам
прибавляется с обеих сторон толщина линии, в первом -
половина толщины линии. Так что это необходимо учитывать,
если нужно знать точное соответствие размеров объекта в
design-time и в run-time (для чего это
может понадобиться - см., например, гл. 11). Однако,
никто не может поручиться, что абсолютно все плееры
ведут себя в этом отношении одинаково (а особенно - что
так же будут вести себя новые версии плеера). Гораздо
более надежно в этих случаях пользоваться формами, или,
что то же самое, заливками (shapes). Об этом
читайте ниже.
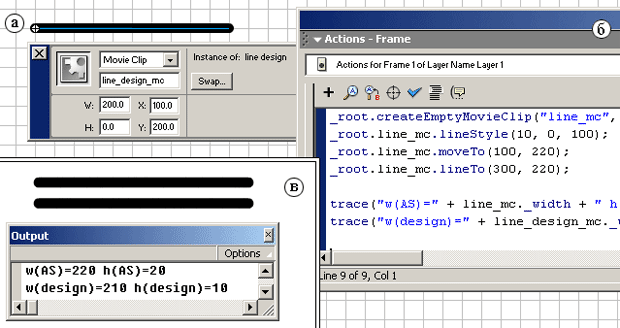
Рис. 10.2.
а) Клип,
содержащий линию и его свойства в design-time;
б) код,
создающий новый клип и рисующий в нем линию, а также
выводящий в Output ширину и высоту этого клипа, и
из пункта а)1)
в)
отображение клипа из пункта а) и результат выполнения
кода из пункта б) в run-time и окно Output.
В примере
10.1 использовались методы
lineStyle, moveTo и
lineTo. Если добавить к
ним еще метод clear (который,
во-первых, стирает все программно нарисованное, а также
сбрасывает настройки, заданные методом
lineStyle), то этого будет
уже достаточно, чтобы рисовать довольно сложные объекты.
Такие, как проекция гиперболоида вращения (пример 10.2),
или бегающая ломаная (пример 10.3), парабола (пример
10.4) или спираль (пример 10.5).
linesNum = 150;
lineRot = 0.35;
xCenter = 275;
HalfWidth = 250;
MinY = 0;
MaxY = 400;
for (var i = 0; i < linesNum; i++){
x1 = xCenter + HalfWidth*Math.sin(2*Math.PI * i / linesNum);
x2 = xCenter + HalfWidth*Math.sin(2*Math.PI *
(i + lineRot*linesNum) / linesNum );
hyper_mc.moveTo(x1, MinY);
hyper_mc.lineTo(x2, MaxY);
}
pointsNum = 6; avSpeed = 20;
globalWidth = 550;
globalHeight = 400;
_root.createEmptyMovieClip("lines_mc", 1);
points = new Array();
for (var i = 0; i < pointsNum; i++){
points.push({x: Math.random()*globalWidth,
y: Math.random()*globalHeight,
vx: 2*avSpeed*(Math.random() - 0.5),
vy: 2*avSpeed*(Math.random() - 0.5)});
}
Пример 10.2.
lines_mc.onEnterFrame =
function(){
for (var i = 0; i < points.length;i++){
points[i].x += points[i].vx;
points[i].y += points[i].vy;
xbound = null;
if (points[i].x < 0) xbound = 0;
if (points[i].x > globalWidth) xbound =
globalWidth;
if (xbound != null){
points[i].x = xbound;
points[i].vx = -points[i].vx
}
ybound = null;
if (points[i].y < 0) ybound = 0;
if (points[i].y > globalHeight) ybound =
globalHeight;
if (ybound != null){
points[i].y = ybound;
points[i].vy = -points[i].vy
}
}
this.clear();
this.lineStyle(1, 0xff0000, 100);
this.moveTo(points[i-1].x, points[i-1].y);
for (var i=0; i< points.length; i++)
this.lineTo(points[i].x, points[i].y);
}
Пример 10.3.
_root.createEmptyMovieClip("curve_mc",
2);
curve_mc.lineStyle(1, 0x00cc00, 100);
var xControl = 50;
var yControl = 100;
var xTarget = 70;
var yTarget = 30;
for (var tau=0; tau <=1; tau+=0.01)
curve_mc.lineTo(2*xControl*tau*(1-tau) + xTarget*tau*tau,
2*yControl*tau*(1-tau) + yTarget*tau*tau);
Пример 10.4.
_root.createEmptyMovieClip("spir_mc",
1);
spir_mc._x = 275; spir_mc._y = 200;
spir_mc.lineStyle(2, 0xcc00ff, 100);
for (var t=0; t<500; t++){
spir_mc.lineTo(0.25*t*Math.cos(0.1*t), 0.25*t*Math.sin(0.1*t));
}
spir_mc.moveTo(0, 0);
for (var t=0; t<500; t++){
spir_mc.lineTo(-0.25*t*Math.cos(0.1*t), -0.25*t*Math.sin(0.1*t));
}
Пример 10.5.
Однако,
кроме этих вышеперечисленных, для рисования линий во
Флэш МХ существует еще один оператор:
curveTo. Давайте
разберемся, для чего он может понадобиться. Из
References, да и просто из названия оператора, можно
понять, что он нужен для рисования плавных кривых. Но
так ли уж необходимо заводить для этого специальный
оператор? Ведь, как видно из примеров 10.4 и 10.5,
плавные кривые можно рисовать, пользуясь только
lineTo.
Однако
давайте посмотрим, что будет, если мы немного
модифицируем код в примере 10.5 и заставим спираль
вращаться. Для этого процесс рисования спирали перенесем
в метод onEnterFrame,
причем каждый раз будем поворачивать ее на небольшой
угол (пример 10.6).
spir_mc.onEnterFrame =
function(){
this.clear();
this.lineStyle(2, 0xcc00ff, 100);
if (curfr == undefined) curfr = 0
else curfr++;
for (var t=0; t<500; t++){
this.lineTo(0.25*t*Math.cos(0.1*t + 0.1*curfr),
-0.25*t*Math.sin(0.1*t + 0.1*curfr));
}
spir_mc.moveTo(0, 0);
for (var t=0; t<500; t++){
this.lineTo(-0.25*t*Math.cos(0.1*t + 0.1*curfr),
0.25*t*Math.sin(0.1*t + 0.1*curfr));
}
}
Пример 10.6.
Полюбуйтесь
на вращающуюся спираль. У вас не закружилась голова?
Тогда посмотрите на загрузку процессора... Дело в том,
что в данном примере в каждом кадре тысячу раз
вызывается оператор lineTo,
следовательно, плееру приходится отображать тысячу
отрезков, каждый из которых - отдельный объект.
Конечно, мы
выбрали экстремальный случай, когда в каждом кадре нужно
перерисовать всю картину. А это требуется не всегда. Так,
в примере 10.7 моделируется поведение броуновской
частицы, и на экране отображается траектория ее движения
(рис 10.3 а). В этом случае в каждом кадре достаточно
дорисовать отрезок траектории частицы, пройденный только
за этот кадр, а всю картину перерисовывать не нужно. То
есть, достаточно только одного оператора
lineTo. Может быть, в этом
случае загрузка процессора будет приемлемой? Однако, не
тут-то было. Посмотрите на рисунок 10.3 б и в. Вверху
(б) показан график зависимости длительности кадра от
количества кадров, прошедших с момента запуска симуляции,
а под ним (в) - график зависимости загрузки процессора
от времени. (Конечно, отображение графика б добавляет в
каждый кадр еще один вызов оператора
lineTo, но качественно на
характер картины это не влияет). Сначала длительность
кадра постоянна - 33 миллисекунды (что соответствует
номинальной скорости проигрывания 30 кадров в секунду).
Но загрузка процессора в это время неуклонно возрастает.
И когда она доходит до ста процентов, начинает
возрастать длительность кадра. То есть, чем больше линий
на экране, тем большее время тратится на перерисовку. Из
этого можно сделать только один вывод: даже если картина
почти не меняется (добавляется один отрезок в несколько
пикселей), флэш-плеер все равно перерисовывает ее
полностью.
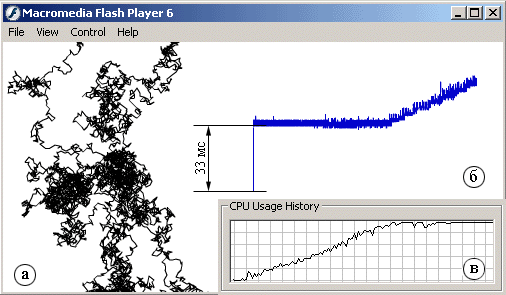
Рис. 10.3. Моделирование поведения броуновской
частицы: а) Траектория движения модели броуновской"
частицы (в каждом кадре меняющей направление своего
движения), изображенная с помощью метода lineTo; б)
график зависимости длительности кадра от номера кадра (тоже
нарисованный с помощью lineTo); в) график зависимости
загрузки процессора от времени при исполнении программы,
отображающей кривые а) и б)
_root.createEmptyMovieClip("brown",
1);
_root.createEmptyMovieClip("timePlot", 2);
curX = 125; curY = 125;
brown.moveTo(curX, curY);
frame = 0;
timePlot._yscale = -100;
timePlot._y = 150;
timePlot._x = 250;
timePlot.lineStyle(1, 0x0000cc, 100);
time = getTimer();
brown.lineStyle(1, 0x000000, 100);
brown.onEnterFrame = function(){
curX += Math.round((Math.random() - 0.5)*10);
curX = curX > 250 ? 250 : ( curX < 0 ? 0 : curX);
curY += Math.round((Math.random() - 0.5)*10);
curY = curY > 250 ? 250 : ( curY < 0 ? 0 : curY);
brown.lineTo(curX, curY);
frame++;
deltaTime = getTimer() - time;
time = getTimer();
timePlot.lineTo(frame, 2*deltaTime);
if (timePlot._width > 250){
timePlot._xscale /=2;
}
}
Пример 10.7.
Можно ли
как-то повлиять на эту ситуацию? В случае примера 10.7 -
боимся, что никак. Разве что каким-нибудь образом
убирать с экрана часть траектории. Однако, это случай
экстремальный: действительно, здесь каждый нарисованный
отрезок никак не связан с предыдущими, и предсказать его
расположение невозможно.
В
большинстве же случаев оптимизация все-таки возможна.
Например, с помощью оператора
curveTo. Давайте несколько модифицируем код из
примера 10.5.
_root.createEmptyMovieClip("spir_mc",
1);
_root.createEmptyMovieClip("spirneg_mc", 2);
spir_mc._x = 275; spir_mc._y = 200;
spir_mc.lineStyle(3, 0xcc00ff, 100);
spirneg_mc._x = 275;
spirneg_mc._y = 200;
spirneg_mc.lineStyle(3, 0xcc00ff, 100);
alpha = 5;
dt = 1;
tmax = 50;
sindt = Math.sin(dt);
cosdt = Math.cos(dt);
cost = 1; sint = 0;
for (var t=0; t<tmax; t+=dt){
R1 = t*t*(cosdt - (t + dt)*sindt) - (t + dt)*(t + dt);
R2 = -t*t*(sindt + (t + dt)*cosdt) + t*(t + dt)*(t + dt);
factor = -alpha /( dt*cosdt + (t*(t+dt) + 1)*sindt);
xc = factor*(R1*cost + R2*sint);
yc = factor*(-R2*cost + R1*sint);
cost = Math.cos(t+dt); sint = Math.sin(t+dt);
xt = alpha*(t+dt)*cost; yt = alpha*(t+dt)*sint;
spir_mc.curveTo(xc, yc, xt, yt);
spirneg_mc.curveTo(-xc, -yc, -xt, -yt);
}
Пример 10.8.
В
результате выполнения этого кода картинка получается
точно такая же, как и в примере 10.5. Однако этот код
выполняется в три раза быстрее.
Оператор
curveTo позволяет не
только ускорить работу программы, но и упростить ее. Так,
цикл for из примера 10.4:
for (var tau=0; tau <=1;
tau+=0.01)
curve_mc.lineTo(2*xControl*tau*(1-tau) + xTarget*tau*tau,
2*yControl*tau*(1-tau) + yTarget*tau*tau);
может быть
заменен одним оператором, как в следующем примере:
curve_mc.curveTo(xControl,
yControl, xTarget, yTarget);
Пример 10.9.
Конечно,
пример 10.4 специально подобран так, чтобы
curveTo так на него
ложилась. Однако, почти любую гладкую кривую можно
достаточно точно аппроксимировать, если грамотно
пользоваться оператором curveTo.
В
References можно прочитать, что оператор
curveTo рисует кривую,
используя текущий стиль линии, начиная от текущей
позиции и заканчивая в точке (xTarget,
yTarget) (имена переменных взяты из примера
10.9), используя контрольную точку
(xControl, yControl). Что
означает эта контрольная точка, разработчики не
конкретизируют, оставляя пользователю простор для
догадок. Однако, с помощью несложного исследования можно
установить, что curveTo
изображает кусок параболы, начинающийся в текущей
позиции и заканчивающийся в (xTarget,
yTarget), такой что касательные в начальной и
конечной точках пересекаются в точке
(xControl, yControl).
Это так
называемая кривая Безье
второго порядка.
Кривая Безье
представляет собой гладкую кривую, построенную по
конечному набору точек на плоскости. Строится она
следующим образом.
Для начала
рассмотрим построение кривой Безье
для трех точек.
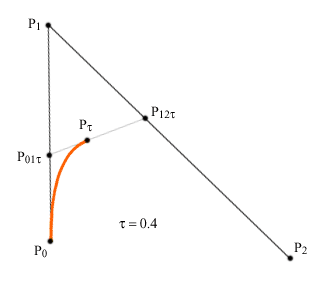
Рис. 10.4.
Пусть на
плоскости заданы три точки P0,
P1 и
P2. Для
определенного значения параметра
τ от 0 до 1 выберем на отрезке
[P0, P1]
точку P01τ,
которая делит отрезок в отношении
τ/(1-τ), на отрезке [P1,
P2] - аналогичную точку
P12τ, и на
получившемся отрезке [P01τ,
P12τ] - точку Pτ,
которая в свою очередь делит отрезок
[P01τ, P12τ]
в отношении τ/(1-τ). Точки
Pτ, полученные
таким образом для всех значений τ
от 0 до 1, и составляют кривую
Безье второго порядка.
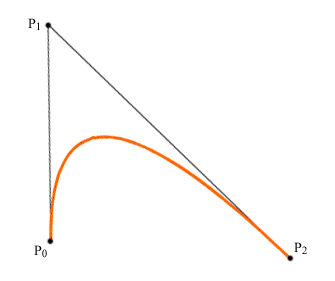
Рис. 10.5.
Нетрудно
показать, что кривая P(τ)
проходит через точки P0
и P2,
касательные к ней в этих точках совпадают с прямыми, на
которых лежат отрезки [P0,
P1] и [P2,
P1], это кривая второго
порядка (парабола),
аналитически в векторном виде записывается следующим
образом:
P =
P0(1 - τ)2
+ 2P1τ(1 - τ) +
P2τ2,
τ
 [0,1]
[0,1]
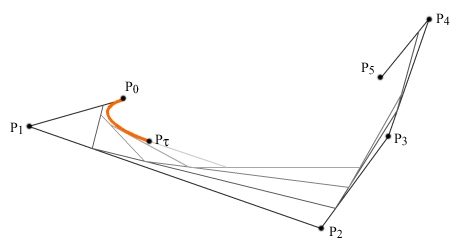
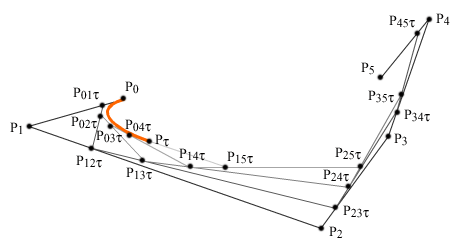
Способ
построения кривой Безье для
произвольного числа точек показан на рис. 10.6 (на
примере шести точек P0
- P5). Так же, как и в рассмотренном
выше случае трех точек, для каждого значения параметра
τ от 0 до 1 найдем
соответствующую этому значению точку кривой (рис.
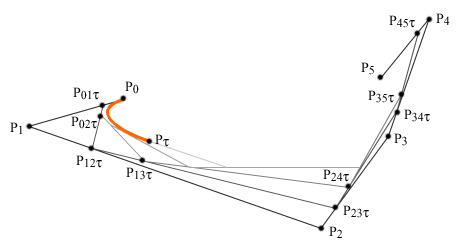
10.6а). Для этого сначала разделим каждый отрезок
ломаной P0 - P5
в отношении τ/(1-τ) (рис.
10.6б). Далее, получившиеся пять точек (P01τ,
P12τ, и т.д.,
см. рис.) соединим отрезками, и каждый из них в свою
очередь разделим в отношении
τ/(1-τ) (рис. 10.6в). Будем повторять эту
процедуру до тех пор, пока у нас не останется один
отрезок P04τ - P15τ
(рис. 10.6г). Точка, которая делит этот
отрезок в отношении τ/(1-τ),
и будет искомой точкой Pτ.
Если изменять значения τ
от 0 до 1 и для каждого находить точку таким образом, то
мы получим кривую Безье
n-го
порядка, где n на 1
меньше числа точек (в данном случае
порядок кривой будет пятый).
Рис. 10.6a.
Рис. 10.6b.
Рис. 10.6c.
Рис. 10.6d.
Можно
доказать, что в аналитическом виде формула
кривой Безье
n-го
порядка выглядит так:
Эта кривая
представляет собой как бы сглаженный вариант ломаной
P0...Pn.
Можно выделить несколько полезных свойств
кривых Безье. Так, эта
кривая всегда проходит через точки
P0 и
Pn. Касательные
к кривой в этих точках совпадают с направлениями
отрезков [P0, P1]
и [Pn-1, Pn]
соответственно. Касательная в произвольной точке
Pτ совпадает с
направлением отрезка [P0(n-1)τ,
P1nτ]. Часть кривой между точками
P0 и
Pτ так же
представляет собой кривую Безье
n-ного
порядка, построенную на
точках [P0, P01τ...P0(n-1)τ,
Pτ]. Аналогично, ост авшаяся часть
кривой - между точками Pτ
и Pn - тоже
является кривой Безье
n-ного
порядка, построенной на
точках [Pτ, P1nτ...P(n-1)nτ,
Pn].
На
практике кривые Безье
применяют для упрощения построения произвольных кривых,
даже не заданных аналитически. Чаще всего для этого
используют кривые Безье
третьего порядка, так
называемые кубические сплайны.
Они достаточно просты для вычислений, но с их помощью
уже можно с хорошей точностью приблизить любую гладкую
кривую. Благодаря этому кривые
Безье третьего порядка
получили широкое распространение в компьютерной графике:
их можно встретить практически в любом редакторе,
позволяющем работать с векторными изображениями. В том
числе в редакторе Flash MX.
Как
нетрудно догадаться, для построения
кривой Безье третьего
порядка нужны четыре точки.
Две точки задают начало и конец кривой (назовем их
опорными), а две другие - направления касательных в
опорных точках, их будем называть контрольными.
Уравнение
кривой Безье третьего
порядка выглядит так:
P =
P0(1 - τ)3
+ 3P1(1 - τ)2τ
+ 3P2(1 - τ)τ2
+ P3τ3,
где
P - точка на кривой,
P0 и
P3 - опорные
точки, P1 и
P2 -
контрольные точки, τ -
параметр, пробегающий значения от 0 до 1. Это уравнение
можно также переписать в виде
P =
P0 + 3(P1
- P0)τ + 3(P2
- 2P1 +
P0)τ2
+ (P3 - 3P2
+ 3P1 -
P0)τ3
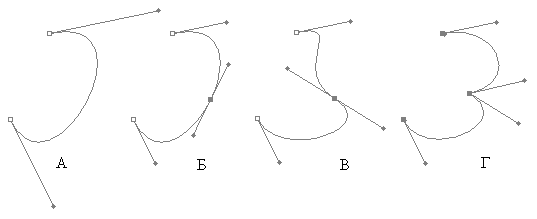
В
редакторах векторной графики пользователь имеет
возможность передвигать опорные и контрольные точки, а
также добавлять на кривую новые опорные точки (рис.
10.7)
При
добавлении новой точки кривая разбивается на две, но в
первый момент это никак не влияет на ее форму (рис. 10.7
Б). Однако получившиеся кривые можно редактировать
независимо, и после редактирования они уже не могут быть
преобразованы обратно в одну
кривую Безье (рис. 10.7 Б и В). Тем не менее,
кривая в этом случае может остаться непрерывной и даже
гладкой - если редактировать контрольные точки так, что
на стыке двух участков опорная точка и две контрольные
оставались на одной прямой (см. рис. 10.7 В), - она и
будет касательной к кривой в данной точке (гладкость
C1).
Рис. 10.7. Редактирование кривой при помощи
кубических сплайнов (Photoshop)
А)
Кривая Безье третьего
порядка
Б) Та же
кривая, разбитая на две части. Обратите внимание, что
контрольные точки на концах исходной кривой стали ближе
к соответствующим опорным, хотя вид кривой не изменился
- дело в том, что они управляют уже не целой кривой, а
только ее частью
В)
Редактирование отдельных частей кривой с сохранением
гладкости в точке соединения
Г)
Редактирование двух частей кривой независимо друг от
друга.
Кривые,
нарисованные в редакторе Flash MX, тоже представляют
собой набор кубических сплайнов.
Опорные точки в них расставляются автоматически (рис.
10.8).
Рис. 10.8. Примеры кривых, нарисованных в
редакторе Flash MX, с опорными точками
Как уже
отмечалось, кубическими сплайнами
можно аппроксимировать кривую любой сложности. Однако,
напомним, что оператор curveTo
рисует кривую Безье второго
порядка. Эта кривая гораздо
проще, чем кубический сплайн,
и для аппроксимации произвольных линий таких кривых
понадобилось бы больше.
Так,
например, для построения окружности (или эллипса) с
хорошей точностью достаточно четырех
кубических сплайнов, а
квадратичных надо как
минимум 10-12 (см. рис. 10.9).
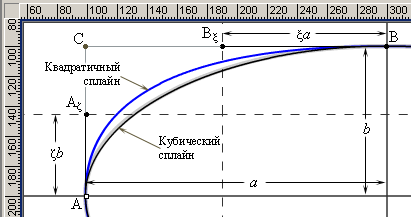
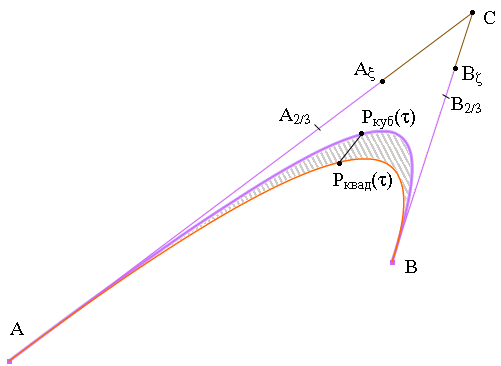
Рис. 10.9. Аппроксимация эллипса при помощи
кубического и квадратичного сплайнов
На рисунке
10.9 эллипс - светло-серая кривая - практически
невозможно отличить от кубического
сплайна (тонкая черная кривая), построенного по
точкам A,
Aζ,
Bξ и
B. Контрольные точки
Aζ и
Bξ подбирались
так, чтобы в точках A и
B совпадали радиусы
кривизны сплайна и исходной
кривой (эллипса). Радиус кривизны кривой вычисляется по
формуле
где точкой
обозначается дифференцирование по параметру. Для эллипса
R(A) = b2/a,
R(A) = a2/b.
Такими же
будут радиусы кривизны в этих точках и для
кубического сплайна, если
взять
ζ = ξ = (√7
- 1)/3.
Квадратичный сплайн (кривая
Безье второго порядка,
построенная по точкам A,
C и
B), как видно на рисунке, в точках
A и
B касается исходной кривой, но в промежутке между
этими точками существенно от нее отклоняется.
Чтобы
аппроксимировать произвольную кривую
квадратичными сплайнами (нарисовать
ее с помощью операторов curveTo),
можно свести задачу к уже решенной: научиться
аппроксимировать кубические
сплайны квадратичными.
Для этого прежде всего попробуем ответить на вопрос:
сколько квадратичных сплайнов
нужно для того, чтобы приблизить один
кубический? Однозначного
ответа на него не существует. Это зависит прежде всего
от относительного расположения опорных и контрольных
точек, а также от необходимой точности. В некоторых
случаях приемлемый результат дает всего один
сплайн. Однако бывает так,
что, независимо от желаемой точности, обойтись одним
сплайном принципиально
невозможно. Так, например, из кривых, представленных на
рис. 10.10, только первую (а) можно было бы
аппроксимировать одним сплайном.
Дело в том, что кривая Безье
второго порядка не содержит
перегибов (рис. 10.10б), поворотов больше чем на 180
градусов (рис. 10.10в) и самопересечений (рис. 10.10г),
а это значит, что для кривых с рис. 10.10 б-г нужно как
минимум по два квадратичных
сплайна.
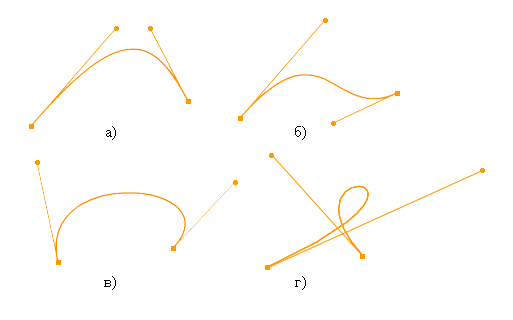
Рис. 10.10. Разнообразные кубические сплайны
Рассмотрим
более подробно случай, когда
кубический сплайн заменяется одним
квадратичным (все остальные
случаи сводятся к нему разбивкой исходного
сплайна на несколько более
мелких).
Рис. 10.11. Кубический и квадратичный сплайны
Пусть у
нас есть кривая Безье
второго порядка:
Pквад(τ)
= А(1 - τ)2 + 2С(1
- τ)τ + Вτ2
и третьего
порядка (рис. 10.11):
Pкуб(τ)
= А(1 - τ)3 + 3Аξ(1
- τ)2τ + 3Вζ(1
- τ)τ2 + Вτ3
Подберем
точку C так, чтобы кривая
Pквад наиболее
точно приближала кривую Pкуб.
Очевидно, что это будет достигнуто, если в опорных
точках кривые будут касаться друг друга. Поскольку в
опорных точках направления касательных к кривым
совпадают с направлением на ближайшую контрольную точку
(это общее свойство кривых Безье),
то это значит, что отрезки AAξ
и AC, а также
BBζ и
BC должны совпадать. Иными
словами, точка C - это
точка пересечения прямых AAξ
и BBζ. И больше
никак на выбор контрольной точки для
квадратичного сплайна мы
повлиять не можем. Теперь следует оценить точность
приближения и, в случае необходимости, разбить
кубический сплайн на два
или более участка, и с каждым из них повторить
вышеописанную процедуру.
Дальше
возникает вопрос: а как оценить точность приближения?
Это можно сделать разными способами.
Так как
точки A,
Aξ и
С лежат на одной прямой,
то можно записать, что
Аξ
= А(1 - ξ) +
Сξ,
где
ξ - действительное число.
Нетрудно видеть, что при ξ = 0
точка Aξ
совпадает с А, а при
ξ = 1 - с точкой
С. Аналогично
Вζ
= В(1 - ζ) +
Сζ.
Надо
заметить, что ξ и
ζ могут быть, вообще
говоря, любыми: и большими единицы, и отрицательными.
Если и ξ, и
ζ отрицательны, то кривая
Pкуб выглядит
так, как на рис. 10.10в, если знаки
ξ и
ζ разные, это соответствует наличию точки
перегиба (рис. 10.10б), если же
1/ξ + 1/ζ < 1,
то кривая
имеет самопересечение (рис. 10.10г).
Если
ζ - ξ = 2/3,
то кривая
Pкуб
вырождается - сокращаются члены, содержащие
τ3 - и
тождественно совпадает с Pквад.
И чем больше ξ и
ζ отличаются от
2/3 в ту или другую
сторону, тем больше расхождение между кривыми. Однако
этот метод расплывчат и мало информативен. В качестве
меры расхождения между кривыми вернее всего было бы
брать максимальное расстояние между ними. Но оно сложно
считается, и разница будет не очень большой, если вместо
него взять максимальное расстояние между точками на двух
кривых при одном и том же значении параметра (на рис.
10.11 показаны точки Pкуб(τ)
и Pквад(τ) для
τ = 1/2). Можно также
использовать площадь заштрихованного на рис. 10.11
участка (взятую по модулю), ее можно посчитать
аналитически.
Если
условия работы программы такие, что отрисовка происходит
намного медленнее, чем расчеты, то можно подумать над
тем, как для каждого кубического
сплайна обойтись не более чем двумя
квадратичными. Для этого
нужно оптимально подобрать значение параметра, по
которому сплайн разбивается на две части - выбрать меру
расхождения (например, площадь "щели" между кривыми),
рассмотреть ее зависимость от точки разбиения и
минимизировать. (Но бывают особые случаи: например, если
есть точка перегиба, то разбивать нужно именно в ней,
потому что участок, содержащий эту точку,
приблизить квадратичным сплайном
нельзя).
Однако
такие ситуации, когда есть ресурсы для сложных расчетов,
но надо экономить на рисовании объектов, встречаются
довольно редко. Поэтому на практике эта задача решается
следующим образом: если точность приближения
недостаточна, сплайн
разбивается на две части в точке
τ =
 и дальше с каждой частью процедура повторяется. В таком
случае получившихся кривых второго
порядка может быть больше, чем при оптимальном
выборе точки, но расчеты существенно упрощаются.
и дальше с каждой частью процедура повторяется. В таком
случае получившихся кривых второго
порядка может быть больше, чем при оптимальном
выборе точки, но расчеты существенно упрощаются.
Но если
перед вами стоит задача изобразить при помощи Флэш МХ
кривую, заданную аналитически, то нет смысла прибегать к
кривым Безье третьего
порядка. Можно сразу
использовать приближение
квадратичными сплайнами. Ведь если у нас есть
формула, задающая кривую (явно или параметрически), это
значит, что мы можем узнать направление касательной в
каждой точке. А если мы знаем направления касательных в
двух не очень удаленных друг от друга точках, то мы
можем соединить эти точки кривой при помощи оператора
curveTo, передавая ему в
качестве аргумента координаты точки пересечения
касательных. Как, например, это было сделано в примере
со спиралью (пример 10.8). Конечно, и здесь надо
аккуратно обходить подводные камни: точки перегиба,
изломы, самопересечения, повороты и другие подобные вещи.
И можно попытаться разработать универсальный алгоритм
разбиения произвольной кривой на точки, включающий в
себя проверку точности приближения, обработку особых
случаев и многое другое Но, как показывает опыт, гораздо
удобнее и оптимальнее (с точки зрения и трудозатрат, и
ресурсоемкости программы при ее выполнении -
быстродействия, памяти и пр.) подбирать свой алгоритм
для каждой конкретной задачи.
Сплошные и градиентные
заливки
Кроме
линий, во Флэш МХ есть возможность рисовать и
протяженные области, залитые одним цветом или градиентом.
Для этого есть методы beginFill,
beginGradientFill и
endFill.
Рассмотрим
сначала сплошную заливку. Она делается при помощи
методов beginFill и
endFill, между вызовами
которых с помощью операторов
lineTo и curveTo
рисуется ограничивающий контур (см. пример 10.10)
(строки
примера пронумерованы, но номера, естественно, не
являются частью кода).
1. _root.createEmptyMovieClip("fill_mc",
1);
2.
3. fill_mc.lineStyle(2, 0x9900ff, 100);
4.
5. fill_mc.beginFill(0xccccff, 100);
6. fill_mc.moveTo(50, 50);
7. fill_mc.lineTo(75, 0);
8. fill_mc.lineTo(100, 50);
9. fill_mc.lineTo(75, 100);
10. fill_mc.lineTo(50, 50);
11. fill_mc.endFill();
12. //--------------
Пример 10.10.
Первый
аргумент beginFill - цвет
заливки (в примере 10.10 0xccccff,
светло-фиолетовый), второй - прозрачность заливки (меняется
от 0 до 100, 0 - полностью прозрачный, 100, как в
примере 10.10 - полностью непрозрачный).
Здесь
следует обратить внимание на несколько вещей. Во-первых,
линия, нарисованная между вызовами
beginFill и
endFill должна быть
непрерывной. То есть, оператор
moveTo может быть вызван только один раз, в
начале. Если он встречается несколько раз, то закрашена
будет только область, нарисованная между последним
вызовом moveTo и вызовом
endFill. Если конечная
позиция контура не совпадает с начальной (если бы в
примере 10.10 не было строчки 10), то при вызове
оператора endFill контур
замыкается прямой линией на начальную позицию (последний
вызов moveTo).
Это
документированное поведение операторов
beginFill и
endFill. Однако при
некоторых условиях результат их выполнения может
оказаться непредсказуемым. (В частности, результат
заливки может зависеть от предыстории - от того, что
делалось в этом клипе до вызова
beginFill. Например, если там не встречалось ни
одного оператора moveTo,
заливка может лишь отдаленно напоминать то, что вы
ожидаете получить.) Чтобы заливка работала устойчиво,
нужно поступать следующим образом. Во-первых, с помощью
moveTo перенести текущую
позицию в начало контура до того, как будет
вызван beginFill,
во-вторых, конечная позиция контура должна совпадать с
начальной.
Между
beginFill и
endFill может быть вызван
метод lineStyle - если
нужно разные части контура рисовать разным стилем. Если
нужна заливка без контура, можно вызвать
lineStyle без аргументов.
FlashMX
позволяет делать заливки не только сплошным цветом, но и
с плавным изменением цвета и прозрачности (градиентом).
Для этого существует метод
beginGradientFill.
Все, что
до сих пор было сказано про
beginFill (кроме описания аргументов),
справедливо и для
beginGradientFill. На аргументах
beginGradientFill
остановимся подробнее.
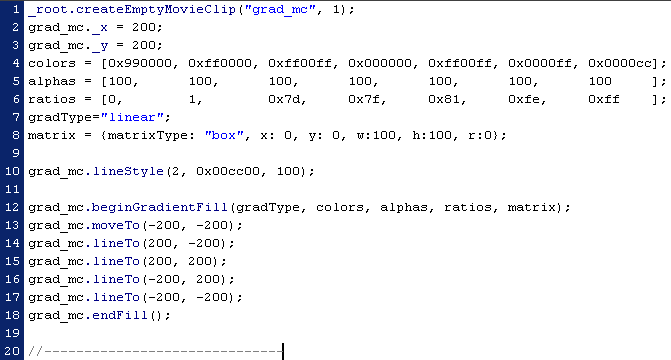
Часть
примера показана в виде скриншота, чтобы сохранить
нумерацию строк.
1. _root.createEmptyMovieClip("grad_mc",
1);
2. grad_mc._x = 200;
3. grad_mc._y = 200;
4. colors = [0x990000, 0xff0000, 0xff00ff, 0x000000,
0xff00ff, 0x0000ff, 0x0000cc];
5. alphas = [100, 100, 100,
100, 100, 100, 100
];
6. ratios = [0, 1,
0x7d, 0x7f, 0x81,
0xfe, 0xff ];
7. gradType="linear";
8. matrix = {matrixType: "box", x: 0, y: 0, w:100,
h:100, r:0};
9.
10. grad_mc.lineStyle(2, 0x00cc00, 100);
11.
12. grad_mc.beginGradientFill(gradType, colors,
alphas, ratios, matrix);
13. grad_mc.moveTo(-200, -200);
14. grad_mc.lineTo(200, -200);
15. grad_mc.lineTo(200, 200);
16. grad_mc.lineTo(-200, 200);
17. grad_mc.lineTo(-200, -200);
18. grad_mc.endFill();
19.
20. //---------------
Пример 10.11.
В
результате выполнения этого кода будет нарисован квадрат
400*400 (его контур обозначен в строчках 13-17), часть
которого будет представлять собой плавный переход одного
цвета в другой. Эти цвета и переход между ними
определяются аргументами метода
beginGradientFill (строчка 12).
Первый
аргумент, gradType (определен
в строке 7) - тип градиента, представляет собой строчку
"linear" или "radial".
В первом случае области одинакового цвета будут
представлять собой параллельные линии, во втором -
эллипсы с одним центром.
Второй
аргумент, colors,
представляет собой массив, члены которого - ключевые
цвета градиента. Цвета, которые находятся между ними,
рассчитываются так, чтобы переход между ключевыми был
линейным.
Третий
аргумент, alphas, - массив
прозрачностей ключевых цветов из массива
colors. Длины этих
массивов должны совпадать.
Четвертый,
ratios, - относительные
положения ключевых цветов градиента. Длина этого массива
должна совпадать с длиной массивов
colors и
alphas. Каждый элемент
массива places
представляет собой число от 0
до 0xff. Если
ratios[i]==0, то цвет,
соответствующий colors[i]
будет располагаться слева в случае градиента типа "linear"
и в центре в случае "radial".
0xff соответствует правому
краю и границе эллипса соответственно. Иными словами,
компонент цвета сj
(R, G или B) зависит от относительного положения
r следующим образом:
cj(r) = colors[i]j
+ (r - ratios[i]j)((colors[i + 1]j
+ colors[i]j)/(ratios[i + 1]j +
ratios[i]j)),
ratios[i]
 r < ratios[i + 1] (10.1)
r < ratios[i + 1] (10.1)
(В формуле
10.1 под colors[i]j
понимается компонент цвета
colors[i], R, G или B, соответствующий
cj).
Аналогичное выражение можно получить и для прозрачности
 : :
 (r)
= alphas[i] + (r - ratios[i])((alphas[i + 1] + alphas[i])/(ratios[i
+ 1] + ratios[i])),
ratios[i] (r)
= alphas[i] + (r - ratios[i])((alphas[i + 1] + alphas[i])/(ratios[i
+ 1] + ratios[i])),
ratios[i]
 r < ratios[i + 1] (10.2)
r < ratios[i + 1] (10.2)
Чтобы
результат выполнения операции
beginGradientFill был предсказуемым, значения в
массиве ratios должны быть
монотонны. Контролировать процесс удобнее, если
ratios[0] равно
0, а последний элемент в
этом массиве равен 0xff,
однако это не обязательно: в противном случае градиент
просто дополняется соответственно первым и последним
элементами массивов colors
и alphas. К сожалению, на
три перечисленных массива есть одно недокументированное
ограничение: их длина не может быть больше 8. Точнее,
может, но учитываются все равно только первые 8
элементов (с номерами от нулевого по седьмой
включительно). Напомним также про необходимость делать
все три массива одинаковой длины.
В примере
10.11 ratios специально
подобраны так, чтобы было видно, где кончается градиент
и начинается сплошной цвет (переход между
0 и
1, а так же между 0xfe
и 0xff выглядит как резкая
граница), а кроме того, в центре присутствует четкая
черная полоска.
И, наконец,
аргумент matrix. Он задает
расположение градиента на экране относительно локальных
координат клипа. Остановимся на нем подробнее.
matrix -
матрица трансформации -
представляет собой объект, который должен содержать либо
поля {a, b, c, d, e, f, g, h, i},
либо {matrixType, w, h, x, y, r},
как в примере 10.11.
Рассмотрим
первый вариант. В этом случае поля объекта
matrix рассматриваются как
матрица 3×3
которая
используется следующим образом.
Предположим, что зависимость компонентов цвета и
прозрачности от координат выражается функциями
cj = fj(x,
y),
 = f
= f (x,
y). Так как cj
и (x,
y). Так как cj
и
 зависят только от относительного положения
r, то достаточно
рассмотреть только функцию
зависят только от относительного положения
r, то достаточно
рассмотреть только функцию
r = ƒ (x, y) (10.4)
В случае
градиента типа "linear"
функция 10.4 принимает вид
ƒ (x, y) = 0xFF • (x + 0.5)
(10.5)
То есть,
от y цвет не зависит, а от
x зависит линейно, при
х = -0.5 r = 0, при
x = 0.5 r = 0xff, так что
весь градиент занимает вертикальную полоску шириной 1.
Если
градиент имеет тип "radial",
то функция 10.4 выглядит так:
ƒ (x, y) = 2 • 0xFF √x2
+ y2 (10.6)
В этом
случае r=0 соответствует
точке (0, 0), а r = 0xFF -
окружности x2 + y2
= 0.25, то есть весть градиент занимает круг с
центром (0, 0) и диаметром 1.
С
практической точки зрения эти функции все еще
бессмысленны - никому не нужен градиент, умещающийся в 1
пиксель.
Преобразуем функцию 10.4 с помощью матрицы 10.3. Эта
матрица описывает такое преобразование
ƒ ƒM,
что обратное к нему ƒM ƒM,
что обратное к нему ƒM ƒ
можно записать через коэффициенты матрицы следующим
образом: ƒ
можно записать через коэффициенты матрицы следующим
образом:
ƒ (x, y) = ƒM(ax +
dy + g,bx + ey + h) (10.7)
(Здесь
реальные экранные координаты - это
x = ax + dy + g,y = bx + ey + h,
а x и
y - аргументы функции 10.5
или 10.6.)
Функция
fnof;M в 10.7
уже задает градиент любого размера и расположения на
экране.
Обратите
внимание, что параметры c,
ƒ и
i в преобразовании 10.7 не используется.
Предполагается, что их значения не меняются:
c = 0,
ƒ = 0 и
i = 1. То есть, матрица
10.3 на самом деле выглядит так:
В
References написано, что в аргументе в объекте
matrix должны
присутствовать все 9 параметров, в том числе
c,
ƒ и i. Однако их
значения (и даже их наличие или отсутствие) на вид
градиента никак не влияют. Возникает естественный вопрос:
если значения этих параметров ни на что не влияют, зачем
вообще о них говорить? В ответ можно привести следующее
рассуждение. Предположим, что функция
ƒ определена не в
двумерном, а в трехмерном пространстве. Тогда
преобразование 10.7 выглядело бы так:
ƒ'(x, y, z) = ƒ'M(ax
+ dy + gz, bx + ey + hz, cz + fy + iz) (10.9)
То есть,
просто представляло бы собой умножение вектора
аргументов (x, y, z) на
матрицу 10.3. Формула 10.7 получается из 10.9, если
положить z
 1. Еще одна причина, чтобы говорить об аргументе
matrix как о матрице 3×3,
- это удобство выполнения последовательных
преобразований. Так, для того, чтобы получить матрицу
преобразования, которое получается последовательным
выполнением двух преобразований с матрицами M1 и
M2, нужно просто перемножить эти матрицы.
1. Еще одна причина, чтобы говорить об аргументе
matrix как о матрице 3×3,
- это удобство выполнения последовательных
преобразований. Так, для того, чтобы получить матрицу
преобразования, которое получается последовательным
выполнением двух преобразований с матрицами M1 и
M2, нужно просто перемножить эти матрицы.
Из 10.10
нетрудно получить, что если матрицы M1 и M2
имеют вид 10.8, то матрица M
тоже имеет вид 10.8:
Не
забывайте: важно, в каком порядке выполняются
преобразования; в данном случае сначала M2 потом
M1 (это справедливо постольку, поскольку мы имеем
дело с обратным преобразованием ƒM
 ƒ. Если бы преобразование было прямым, то запись
10.11 означала бы, что выполняется сначала M1
потом M2).
ƒ. Если бы преобразование было прямым, то запись
10.11 означала бы, что выполняется сначала M1
потом M2).
Связь
между компонентами матрицы 10.3 и параметрами градиента
на первый взгляд кажется неочевидной. Чтобы это
прояснить, рассмотрим несколько примеров.
Пусть
матрица М имеет вид
Тогда
преобразование градиента будет ƒ
(x, y) = ƒM(W • x, H • y), то есть
r(x, y) = ƒM(x, y) =
255 • (x/W) + 0.5в случае градиента "linear"
r(x, y) = ƒM(x, y) =
255 • 0.5 √(x/W)2 + (y/H)2в
случае "radial".
Таким
образом, градиент просто растягивается в ширину на
W и в высоту на
H пикселей.
Чтобы
проверить, как это будет выглядеть на экране, можно
воспользоваться следующим примером:
_root.createEmptyMovieClip("grad_mc",
1);
grad_mc._x = 200;
grad_mc._y = 200;
colors = [0xffffff, 0x000000, 0xffffff, 0x000000,
0xffffff, 0xcccccc, 0xffffff];
alphas = [100, 100, 100,
100, 100, 100,
100 ];
ratios = [0, 1,
0x7d, 0x7f, 0x81,
0xfe, 0xff ];
//Задаем компоненты матрицы.
//Чтобы задать новую матрицу, достаточно будет
изменить эти строчки.
a0 = 100; b0 = 0;
d0 = 0; e0 = 50;
g0 = 0; h0 = 0;
//-------------
gradType="radial"; //Задаем тип градиента
// Создаем матрицу
matrix = {a: _root.a0, b: _root.b0,
d: _root.d0, e: _root.e0,
g: _root.g0, h: _root.h0}
grad_mc.clear();
grad_mc.lineStyle(2, 0x00cc00, 100);
//Рисуем заливку градиентом
grad_mc.beginGradientFill(gradType, colors, alphas,
ratios, matrix);
grad_mc.moveTo(-200, -200);
grad_mc.lineTo( 200, -200);
grad_mc.lineTo( 200, 200);
grad_mc.lineTo(-200, 200);
grad_mc.lineTo(-200, -200);
grad_mc.endFill();
//------------
// Кроме градиента нарисуем еще вспомогательный
четырехугольник,
// в который превращается квадрат [-0.5<x<0.5,
-0.5<y<0.5]
// после преобразования,задаваемого матрицей
matrix.
with (matrix){
grad_mc.lineStyle(0, 0x808080, 100);
grad_mc.moveTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
grad_mc.lineTo(0.5*(-a + d) + g, 0.5*(-b + e) + h);
grad_mc.lineTo(0.5*( a + d) + g, 0.5*( b + e) + h);
grad_mc.lineTo(0.5*( a - d) + g, 0.5*( b - e) + h);
grad_mc.lineTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
}
Пример 10.12.

Рис. 10.12.
Результат
применения матрицы 10.12 (W = 100,
H = 50) для
линейного и
радиального градиентов (код
приведен в примере 10.12).
Для
поворота градиента на угол по часовой стрелке служит
матрица следующего вида:
Матрица
последовательного выполнения масштабирования и поворота
будет выглядеть так:
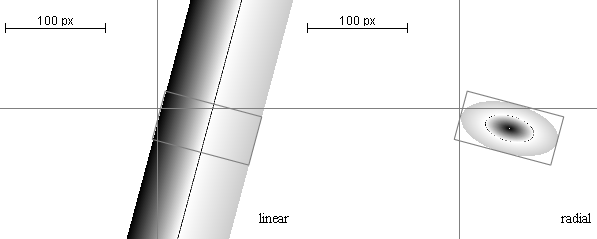
Рис. 10.13.
Результат
применения матрицы 10.14 (W = 100,
H = 50,
 =
=
 *0.1)
для линейного и
радиального градиентов. *0.1)
для линейного и
радиального градиентов.
Поворот и
масштабирование оставляют на месте центр градиента.
Переместить этот центр затем можно с помощью матрицы
следующего вида:
Для
выполнения масштабирования, поворота и смещения служит
матрица
Рис. 10.14.
Результат
применения матрицы 10.16 (W = 100,
H = 50,
 = 0.1
= 0.1 ,
x0 = 50,
y0 = 20) для
линейного и
радиального градиентов. ,
x0 = 50,
y0 = 20) для
линейного и
радиального градиентов.
Матрица
вида 10.16 наиболее очевидно и естественно описывает
любое возможное расположение градиента. Это градиент,
умещающийся в прямоугольник высотой
H и шириной
W, повернутый по часовой
стрелке на угол
 ,
с центром в точке (x0,
y0). Никакого более сложного градиента
на Flash МХ сделать невозможно. ,
с центром в точке (x0,
y0). Никакого более сложного градиента
на Flash МХ сделать невозможно.
Если
приглядеться к матрице 10.16 повнимательнее, можно
заметить, что там используется только 5 независимых
параметров: W,
H,
x0, y0,
и
 .
Однако в объекте matrix,
который является аргументом метода
beginGradientFill, их
может быть шесть. Действительно, преобразование 10.16
оставляет исходный квадрат [-0.5
< x < 0.5, -0.5 < y < 0.5] прямоугольником, а в
общем же случае он становится параллелограммом. Тем не
менее к противоречию с тем, что сказано выше, это не
приводит. В этом легко убедиться, если для произвольной
матрицы вида 10.8 подобрать матрицу вида 10.16 с
параметрами .
Однако в объекте matrix,
который является аргументом метода
beginGradientFill, их
может быть шесть. Действительно, преобразование 10.16
оставляет исходный квадрат [-0.5
< x < 0.5, -0.5 < y < 0.5] прямоугольником, а в
общем же случае он становится параллелограммом. Тем не
менее к противоречию с тем, что сказано выше, это не
приводит. В этом легко убедиться, если для произвольной
матрицы вида 10.8 подобрать матрицу вида 10.16 с
параметрами
 = atan2 (-d, e);
= atan2 (-d, e);
W = (ae - bd)/(√e2 + d2);
H = √e2 + d2;
x0 = g;
y0 = h (10.17)
для
линейного градиента, и с
параметрами
 = 0.5 • atan2 (2(ab + ed), a2 - b2
+ d2 - e2);
= 0.5 • atan2 (2(ab + ed), a2 - b2
+ d2 - e2);
W = Δ/√S - L;
H = Δ/√S + L;
x0 = g;
y0 = h (10.18)
где
Δ = ae - bd;
S = 0.5 (a2 + b2 + d2
+ e2);
L = √S2 - Δ2;
для
радиального. Градиент,
построенный по этой матрице, будет идентичен исходному.
Проверить это можно, слегка изменив код из примера
10.12:
matrix = {a: _root.a0, b:
_root.b0,
d: _root.d0, e: _root.e0,
g: _root.g0, h: _root.h0}
with (matrix){
_root.delta = a*e - b*d;
if (gradType == "radial"){
S=0.5*(e*e + a*a + d*d + b*b);
L=Math.sqrt(S*S-delta*delta);
h1 = delta / Math.sqrt(L + S);
w1 = delta / Math.sqrt(S - L);
phi1 = 0.5*Math.atan2( 2*(e*d + a*b), d*d + a*a -
e*e - b*b );
} else {
h1=Math.sqrt(e*e + d*d);
w1=delta/h1;
phi1=Math.atan2(-d, e);
}
}
matrix1 = {a: w1*Math.cos(phi1), b:
w1*Math.sin(phi1),
d:-h1*Math.sin(phi1), e:
h1*Math.cos(phi1),
g: _root.g0,
h: _root.h0}
grad_mc.beginGradientFill(gradType, colors, alphas,
ratios, matrix1);
grad_mc.moveTo(-200, -200);
grad_mc.lineTo( 200, -200);
grad_mc.lineTo( 200, 200);
grad_mc.lineTo(-200, 200);
grad_mc.lineTo(-200, -200);
grad_mc.endFill();
with (matrix){
grad_mc.lineStyle(0, 0x808080, 100);
grad_mc.moveTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
grad_mc.lineTo(0.5*(-a + d) + g, 0.5*(-b + e) + h);
grad_mc.lineTo(0.5*( a + d) + g, 0.5*( b + e) + h);
grad_mc.lineTo(0.5*( a - d) + g, 0.5*( b - e) + h);
grad_mc.lineTo(0.5*(-a - d) + g, 0.5*(-b - e) + h);
}
Пример 10.13.
В этом
примере градиент строится по матрице
matrix1 вида 10.16, а
ограничивающий прямоугольник - по исходной матрице
matrix. Нетрудно убедиться,
что градиент оказывается вписанным в четырехугольник при
любых параметрах исходной матрицы.
Рассмотрим
теперь градиент с матрицей вида типа "box":
{matrixType, w, h, x, y, r}.
На первый взгляд может показаться, что поля такого
объекта похожи на параметры матрицы 10.16, но это не
совсем так. Матрица преобразования для такого градиента
имеет вид:
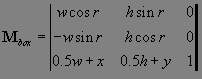
Преобразования, соответствующие этой матрице, следующие:
сначала - сдвиг по x и по
y на 0.5 (то есть, левый
верхний угол прямоугольника, содержащего градиент,
оказывается в точке (0, 0)), затем поворот на угол
r (в радианах), затем
растяжение по x в
w и по
y в
h раз. Это преобразование отличается от
преобразования по матрице 10.16 наличием сдвига на 0.5
по х и
y, а главное - порядком
операций поворота и масштабирования. И эта разница
существенна. Так, если выполнять преобразование 10.19
для радиального градиента,
то поворот осуществляется тогда, когда градиент еще
имеет радиальную симметрию, а значит его форма при
повороте не меняется. То есть, с помощью такого
преобразования мы можем получить только эллипс с осями,
параллельными осям координат (рис. 10.13). Расположение
линейного градиента при
таком способе задания оказывается трудно предсказуемым (кроме
самых простых случаев, когда r =
0 или w = h).
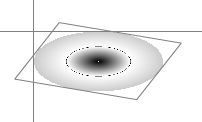
Рис. 10.15.
Результат
выполнения метода
beginGradientFill с аргументом
matrix = {matrixType: "box", w:
130, h:60, x: 0, y: 0, r: Math.PI/180*20}
Как было
сказано выше, с помощью одного оператора
beginGradientFill во
FlashMX можно получить только эллиптический или
линейный градиент. Однако
если наложить друг на друга несколько градиентов с
изменением прозрачности, то можно получить переход цвета
довольно сложной формы. Один из таких вариантов
рассмотрен в примере 10.14.
outlineSqr = function(){
moveTo(-100, -100);
lineTo(100, -100);
lineTo(100, 100);
lineTo(-100, 100);
lineTo(-100, -100);
}
beginFill(0, 100);
outlineSqr();
endFill();
beginGradientFill("linear",
[0xffffff,0xffffff, 0xfffffff],
[100, 0, 100],
[0, 0x7f, 0xFF],
{a: 200, b: 0, d: 0, e: 200, g: 0, h:0});
outlineSqr();
endFill();
beginGradientFill("linear",
[0xffffff,0xffffff, 0xfffffff],
[100, 0, 100],
[0, 0x7f, 0xFF],
{a: 0, b: 200, d: -200, e: 0, g: 0, h:0});
outlineSqr();
endFill();
Пример 10.14.
Рис. 10.16. Результат выполнения кода из примера
10.14
Примеров
практического применения программно нарисованной
градиентной заливки может
быть много. Приведем здесь один из них: динамический
градиент удобно использовать, если нужно размыть края
произвольной картинки плавным переходом в цвет фона.
Сделать это можно несколькими способами. Самый простой
из них описан в примере 10.15.
makeFeatherFrame =
function(target_mc, width, color){
boundRect=target_mc.getBounds();
targDepth = getMaxFreeDepth(target_mc);
frName = target_mc._name + "_frame";
target_mc.createEmptyMovieClip(frName, targDepth);
frame_mc = target_mc[frname];
frame_mc._x = boundRect.xMin;
frame_mc._y = boundRect.yMin;
W = boundRect.xMax - boundRect.xMin;
H = boundRect.yMax - boundRect.yMin;
relHorWidth = 0xFF * width / W;
relVerWidth = 0xFF * width / H;
colors = [color, color, color, color];
alphas = [100, 0, 0, 100];
horRatios = [0, relHorWidth, 0xFF - relHorWidth, 0xFF];
verRatios = [0, relVerWidth, 0xFF - relVerWidth, 0xFF];
horMatrix = {a: W, b: 0, d: 0, e: H, g: W/2, h: H/2};
verMatrix = {a: 0, b: H, d: -W, e: 0, g: W/2, h: H/2};
frame_mc.beginGradientFill("linear", colors, alphas,
horRatios, horMatrix);
outlineRect(frame_mc, 0, 0, W, H);
frame_mc.endFill();
frame_mc.beginGradientFill("linear", colors, alphas,
verRatios, verMatrix);
outlineRect(frame_mc, 0, 0, W, H);
frame_mc.endFill();
}
getMaxFreeDepth = function(target_mc){
var mfd = 0;
for (in_mc in target_mc){
if (typeof(target_mc[in_mc])=="movieclip"
&& target_mc[in_mc].getDepth() > mfd)
mfd = target_mc[in_mc].getDepth();
}
return mfd + 1;
}
outlineRect = function(target_mc, xMin, yMin, xMax,
yMax){
target_mc.moveTo(xMin, yMin);
target_mc.lineTo(xMin, yMax);
target_mc.lineTo(xMax, yMax);
target_mc.lineTo(xMax, yMin);
target_mc.lineTo(xMin, yMin);
}
makeFeatherFrame(photo_mc, 30, 0xffffff);
Пример 10.15.

Рис. 10.17. Результат выполнения кода из примера
10.15
На этом
примере обнаруживается еще одно ограничение
динамического градиента: пространство между крайними
цветами градиента делится на 255 (0xFF) частей, и каждая
часть заливается сплошным цветом. И чем шире градиент,
тем шире - а следовательно заметнее - каждая полоска.
Так что на краях фотографии, показанной на рисунке
10.17, можно заметить, что цвет фотографии в цвет фона
переходит не плавно, особенно на правой и левой границах.
Чтобы этого избежать, можно делать
градиентную заливку не на всей ширине клипа, а
только на границах. Это, однако, увеличивает количество
кода (пример 10.16).
makeStrictFeatherFrame =
function(target_mc, width, color){
boundRect=target_mc.getBounds();
// метод getMaxFreeDepht описан в предыдущем примере
targDepth = getMaxFreeDepth(target_mc);
frName = target_mc._name + "_frame";
target_mc.createEmptyMovieClip(frName, targDepth);
frame_mc = target_mc[frname];
frame_mc._x = boundRect.xMin;
frame_mc._y = boundRect.yMin;
W = boundRect.xMax - boundRect.xMin;
H = boundRect.yMax - boundRect.yMin;
colors = [color, color];
alphas = [100, 0];
ratios = [0, 0xFF];
lMatrix = {a: width, b: 0, d: 0, e: 100, g: width/2,
h: H/2};
tMatrix = {a: 0, b: width, d: -100, e: 0, g: W/2, h:
width/2};
rMatrix = {a: -width, b: 0, d: 0, e: -100, g: W -
width/2, h: H/2};
bMatrix = {a: 0, b: -width, d: 100, e: 0, g: W/2, h:
H - width/2};
with (frame_mc){
beginGradientFill("linear", colors, alphas, ratios, lMatrix);
//метод outlineRect описан в предыдущем примере
outlineRect(frame_mc, 0, 0, width, H);
endFill();
beginGradientFill("linear", colors, alphas, ratios, tMatrix);
outlineRect(frame_mc, 0, 0, W, width);
endFill();
beginGradientFill("linear", colors, alphas, ratios, rMatrix);
outlineRect(frame_mc, W-width, 0, W, H);
endFill();
beginGradientFill("linear", colors, alphas, ratios, bMatrix);
outlineRect(frame_mc, 0, H-width, W, H);
endFill();
}
}
makeStrictFeatherFrame(photo_mc, 30, 0xffffff);
Пример 10.16.

Рис. 10.18. Результат выполнения кода из примера
10.16
В примере
10.16 расстояние, на котором происходит переход одного
цвета в другой, определяется толщиной рамки, так что на
рис. 10.18 дискретность градиента не заметна. Однако
если приглядеться к углам фотографии, они могут
показаться все еще неудовлетворительными: в каждом углу
наблюдается картинка, похожая на рис. 10.14. Чтобы этого
избежать, можно дополнить линейные
градиенты по сторонам фотографии радиальными в ее
углах (пример 10.17).
makeStrictRoundedFeatherFrame
= function(target_mc, width, color){
boundRect=target_mc.getBounds();
targDepth = getMaxFreeDepth(target_mc);
frName = target_mc._name + "_frame";
target_mc.createEmptyMovieClip(frName, targDepth);
frame_mc = target_mc[frname];
frame_mc._x = boundRect.xMin;
frame_mc._y = boundRect.yMin;
W = boundRect.xMax - boundRect.xMin;
H = boundRect.yMax - boundRect.yMin;
colors = [color, color];
alphas = [0, 100];
ratios = [0, 0xFF];
lMatrix = {a: -width, b: 0, d: 0, e: 100, g:
width/2, h: H/2};
tMatrix = {a: 0, b: -width, d: -100, e: 0, g: W/2,
h: width/2};
rMatrix = {a: width, b: 0, d: 0, e: -100, g: W -
width/2, h: H/2};
bMatrix = {a: 0, b: width, d: 100, e: 0, g: W/2, h:
H - width/2};
ltMatrix = {a: 2*width, b: 0, d: 0, e: 2*width, g:
width, h: width};
rtMatrix = {a: 2*width, b: 0, d: 0, e: 2*width, g:
W-width, h: width};
rbMatrix = {a: 2*width, b: 0, d: 0, e: 2*width, g:
W-width,
h: H-width};
lbMatrix = {a: 2*width, b: 0, d: 0, e: 2*width, g:
width,
h: H-width};
with (frame_mc){
beginGradientFill("linear", colors, alphas, ratios, lMatrix);
outlineRect(frame_mc, 0, width, width, H-width);
endFill();
beginGradientFill("linear", colors, alphas, ratios, tMatrix);
outlineRect(frame_mc, width, 0, W-width, width);
endFill();
beginGradientFill("linear", colors, alphas, ratios, rMatrix);
outlineRect(frame_mc, W-width, width, W, H-width);
endFill();
beginGradientFill("linear", colors, alphas, ratios, bMatrix);
outlineRect(frame_mc, width, H-width, W-width, H);
endFill();
beginGradientFill("radial", colors, alphas, ratios, ltMatrix);
outlineRect(frame_mc, 0, 0, width, width);
endFill();
beginGradientFill("radial", colors, alphas, ratios, rtMatrix);
outlineRect(frame_mc, W-width, 0, W, width);
endFill();
beginGradientFill("radial", colors, alphas, ratios, rbMatrix);
outlineRect(frame_mc, W-width, H-width, W, H);
endFill();
beginGradientFill("radial", colors, alphas, ratios, lbMatrix);
outlineRect(frame_mc, 0, H-width, width, H);
endFill();
}
}
Пример 10.17.

Рис. 10.19. Результат выполнения кода из примера
10.17
Граница
фотографии на рис. 10.19 выглядит вполне аккуратно,
однако количество кода в примере 10.17 еще больше.
Градиент
типа "radial" можно
использовать для получения овальной рамки (пример
10.18).
makeOvalFrame =
function(target_mc, width, color){
boundRect=target_mc.getBounds(target_mc._parent);
targDepth = target_mc.getDepth();
frName = target_mc._name + "_frame";
target_mc._parent.createEmptyMovieClip(frName, targDepth+1);
frame_mc = target_mc._parent[frname];
frame_mc._x = boundRect.xMin;
frame_mc._y = boundRect.yMin;
W = boundRect.xMax - boundRect.xMin;
H = boundRect.yMax - boundRect.yMin;
relWidth = 2*0xFF * width / Math.max(W, H);
colors = [color, color, color];
alphas = [0, 0, 100];
ratios = [0, 0xFF - relWidth, 0xFF];
matrix = {a: W, b: 0, d: 0, e: H, g: W/2, h: H/2};
frame_mc.beginGradientFill("radial", colors, alphas, ratios,
matrix);
outlineRect(frame_mc, 0, 0, W, H);
frame_mc.endFill();
}
Пример 10.18.
Рис. 10.20. Результат выполнения кода из примера
10.18
1) Объекты
из пунктов а и б на первый взгляд могут показаться
частями одного скриншота. Но на самом деле это монтаж,
от редактора Flash MX такого добиться невозможно: если
на сцене выделен какой-то объект, то в панели Actions
показывается код, относящийся к этому объекту. Однако на
рисунке в панели Actions отображен код,
относящийся к кадру. |
 Посмотреть
порно видео в онлайне »
Посмотреть
порно видео в онлайне »